
分析 根据考试的成绩ξ服从正态分布N(110,102).得到考试的成绩ξ关于ξ=110对称,根据P(100≤ξ≤110)=0.36,得到P(ξ≥120)=0.14,根据频率乘以样本容量得到这个分数段上的人数.
解答 解:∵考试的成绩ξ服从正态分布N(110,102).
∴考试的成绩ξ关于ξ=110对称,
∴P=(ξ>120)=0.5-P(100≤ξ≤110)=0.5-0.36=0.14,
所以估计该班学生数学成绩在120分以上的人数为50×0.14=7(人).
故答案为:7.
点评 本题考查正态曲线的特点及曲线所表示的意义,是一个基础题,解题的关键是考试的成绩ξ关于ξ=110对称,利用对称写出要用的一段分数的频数,题目得解.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1) | B. | (-1,+∞) | C. | (0,$\frac{1}{e}$) | D. | ($\frac{1}{e}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
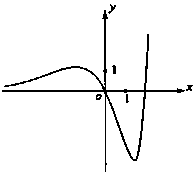
| A. | a=1,b=2 | B. | a=1,b=-2 | C. | a=-1,b=2 | D. | a=-1,b=-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com