
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | 2 |
分析 求出f(x)的导数,求得x=1处的切线的斜率,再由基本不等式,可得斜率的最小值,求出满足的条件,解方程可得a的值.
解答 解:f(x)=2ax2-$\frac{1}{ax}$的导数为f′(x)=4ax+$\frac{1}{a{x}^{2}}$,
可得在点(1,f(1))处的切线的斜率为k=4a+$\frac{1}{a}$,
由a>0,可得4a+$\frac{1}{a}$≥2$\sqrt{4a•\frac{1}{a}}$=4,
当且仅当4a=$\frac{1}{a}$,即a=$\frac{1}{2}$时,k取最小值.
故选:A.
点评 本题考查导数的运用:求切线的斜率,考查最值的求法,注意运用基本不等式,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
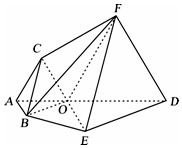 如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
如图,ABEDEFC为多面体,平面ABED⊥平面ACED,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.
如图,直三棱柱ABC-A1B1C1中,AC⊥AB,AB=2AA1,M是AB的中点,△A1MC1是等腰三角形,D为CC1的中点,E为BC上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com