
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为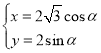 (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() ,且
,且![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,已知点
两点,已知点![]() 的极坐标为
的极坐标为![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程,并求
的直角坐标方程,并求![]() 的值;
的值;
(2)若矩形![]() 内接于曲线
内接于曲线![]() 且四边与坐标轴平行,求其周长的最大值.
且四边与坐标轴平行,求其周长的最大值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】垃圾分类是改善环境,节约资源的新举措.住建部于6月28日拟定了包括我市在内的46个重点试点城市,要求这些城市在2020年底基本建成垃圾分类处理系统.为此,我市某中学对学生开展了“垃圾分类”有关知识的讲座并进行测试,将所得测试成绩整理后,绘制出频率分布直方图如图所示.

(1)求频率分布直方图中a的值,并估计测试的平均成绩;
(2)将频率视为相应的概率,如果从参加测试的同学中随机选取4名同学,这4名同学中测试成绩在![]() 的人数记为
的人数记为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“公平正义”是社会主义和谐社会的重要特征,是社会主义法治理念的价值追求.“考试”作为一种公平公正选拔人才的有效途径,正被广泛采用.每次考试过后,考生最关心的问题是:自己的考试名次是多少?自已能否被录取?能获得什么样的职位?
某单位准备通过考试(按照高分优先录取的原则)录用![]() 名,其中
名,其中![]() 个高薪职位和
个高薪职位和![]() 个普薪职位.实际报名人数为
个普薪职位.实际报名人数为![]() 名,考试满分为
名,考试满分为![]() 分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
分. 考试后对部分考生考试成绩进行抽样分析,得到频率分布直方图如下:
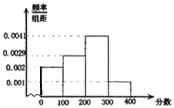
试结合此频率分布直方图估计:
(1)此次考试的中位数是多少分(保留为整数)?
(2)若考生甲的成绩为280分,能否被录取?若能被录取,能否获得高薪职位?(分数精确到个位,概率精确到千分位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在矩形![]() 中,
中,![]() 为边
为边![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 折起到
折起到![]() (
(![]() 平面
平面![]() )的位置,
)的位置,![]() 为线段
为线段![]() 的中点.
的中点.
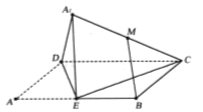
(1)求证:![]() 平面
平面![]() ;
;
(2)已知![]() ,当平面
,当平面![]() 平面
平面![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() ,在以坐标原点为极点,
,在以坐标原点为极点,![]() 轴的非负半轴为极轴的极坐标系中,曲线
轴的非负半轴为极轴的极坐标系中,曲线![]() 的方程为
的方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,设点
两点,设点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,已知![]() ,顶点P在平面ABC上的射影为
,顶点P在平面ABC上的射影为![]() 的外接圆圆心.
的外接圆圆心.
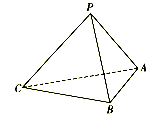
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若点M在棱PA上,![]() ,且二面角P-BC-M的余弦值为
,且二面角P-BC-M的余弦值为![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com