
如图,F是中心在原点、焦点在x轴上的椭圆C的右焦点,直线l:x=4是椭圆C的右准线,F到直线l的距离等于3.
(1)求椭圆C的方程;
(2)点P是椭圆C上动点,PM⊥l,垂足为M.是否存在点P,使得△FPM为等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.

(1)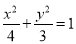 ;(2)P(
;(2)P(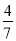 ,±
,±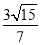 ).
).
【解析】
试题分析:(1)求椭圆标准方程,一般利用待定系数法,利用两个独立条件确定a,b的值. 设椭圆C的方程为 ,由已知,得
,由已知,得 ,∴
,∴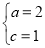 ∴b=
∴b=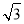 .所以椭圆C的方程为
.所以椭圆C的方程为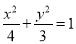 .(2)等腰三角形这个条件,是不确定的,首先需要确定腰. 由
.(2)等腰三角形这个条件,是不确定的,首先需要确定腰. 由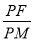 =e=
=e=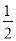 ,得PF=
,得PF=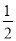 PM.∴PF≠PM.若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与FM相等.因此只有FM=PM,然后结合点在椭圆上条件进行列方程求【解析】
PM.∴PF≠PM.若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,∴PF不可能与FM相等.因此只有FM=PM,然后结合点在椭圆上条件进行列方程求【解析】
设P(x,y)(x≠±2),则M(4,y).∴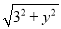 =4-x,
=4-x,
∴9+y2=16-8x+x2,又由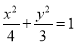 ,得y2=3-
,得y2=3-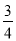 x2.∴9+3-
x2.∴9+3-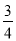 x2=16-8x+x2,∴
x2=16-8x+x2,∴ x2-8x+4=0.∴7x2-32x+16=0.∴x=
x2-8x+4=0.∴7x2-32x+16=0.∴x= 或x=4.∵x∈(-2,2),∴x=
或x=4.∵x∈(-2,2),∴x=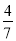 .∴P(
.∴P( ,±
,±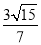 ).综上,存在点P(
).综上,存在点P(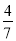 ,±
,±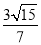 ),使得△PFM为等腰三角形.
),使得△PFM为等腰三角形.
试题解析:【解析】
(1)设椭圆C的方程为
由已知,得 ,∴
,∴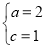 ,∴b=
,∴b=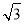 .所以椭圆C的方程为
.所以椭圆C的方程为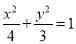
(2)由 =e=
=e=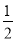 ,得PF=
,得PF=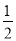 PM.∴PF≠PM.
PM.∴PF≠PM.
①若PF=FM,则PF+FM=PM,与“三角形两边之和大于第三边”矛盾,
∴PF不可能与FM 相等.
②若FM=PM,设P(x,y)(x≠±2),则M(4,y).∴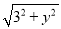 =4-x,
=4-x,
∴9+y2=16-8x+x2,又由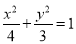 ,得y2=3-
,得y2=3- x2.∴9+3-
x2.∴9+3-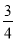 x2=16-8x+x2,
x2=16-8x+x2,
∴ x2-8x+4=0.∴7x2-32x+16=0.∴x=
x2-8x+4=0.∴7x2-32x+16=0.∴x= 或x=4.∵x∈(-2,2),∴x=
或x=4.∵x∈(-2,2),∴x=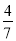 .
.
∴P( ,±
,± ).综上,存在点P(
).综上,存在点P(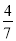 ,±
,± ),使得△PFM为等腰三角形.
),使得△PFM为等腰三角形.
考点:椭圆方程,椭圆第二定义


科目:高中数学 来源:2015届江苏省南京市高三9月调研考试理科数学试卷(解析版) 题型:解答题
已知矩阵A= 属于特征值?的一个特征向量为α=
属于特征值?的一个特征向量为α= .
.
(1)求实数b,?的值;
(2)若曲线C在矩阵A对应的变换作用下,得到的曲线为C?:x2+2y2=2,求曲线C的方程.
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京市高二下4月月考数学试卷(解析版) 题型:填空题
“ ”是“
”是“ ”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)
”的___________条件.(用“充要”“充分不必要”“必要不充分”“既不充分也不必要”填空)
查看答案和解析>>
科目:高中数学 来源:2015届江苏省南京外国语学校高二上学期期中测试数学试卷(解析版) 题型:填空题
对任意实数λ,直线l1:x+λy-m-λn=0与圆C:x2+y2=r2总相交于两不同点,则直线l2:mx+ny=r2与圆C的位置关系是 .
查看答案和解析>>
科目:高中数学 来源:2015届江苏省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路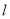 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.
(1)当 时,求直路
时,求直路 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?

查看答案和解析>>
科目:高中数学 来源:2015届江苏无锡洛社高级中学高二下学期期中考试文科数学卷(解析版) 题型:解答题
已知命题:“ ,使等式
,使等式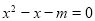 成立”是真命题.
成立”是真命题.
(1)求实数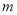 的取值集合
的取值集合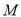 ;
;
(2)设不等式 的解集为
的解集为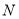 ,若
,若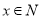 是
是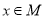 的必要条件,求
的必要条件,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com