考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的综合应用
分析:(Ⅰ)通过a=1,求出函数的导数,利用导数为0求出极值点,判断导函数的符号即可求解函数单调区间;
(Ⅱ) 求出函数的导数,求解极值点,转化在区间[1,e]上至少存在一点x0,使得f(x0)<0成立,为求解函数的最值问题,利用a的取值范围的讨论,求解函数的最值,即可求得实数a的取值范围.
解答:
解:(I)因为
f′(x)=-+=,…(2分)
当a=1,
f′(x)=,令f'(x)=0,得 x=1,又f(x)的定义域为(0,+∞),f'(x),f(x)随x的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
所以x=1时,f(x)的极小值为1.…(4分)f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1); …(5分)
(II)因为
f′(x)=-+=,且a≠0,令f'(x)=0,得到
x=,
若在(0,e]上存在一点x
0,使得f(x
0)<0成立,其充要条件是f(x)在区间(0,e]上的最小值小于0即可.(1)当
x=<0,即a<0时,f'(x)<0对x∈(0,+∞)成立,所以f(x)在区间(0,e]上单调递减,
故f(x)在区间(0,e]上的最小值为
f(e)=+alne=+a,
由
+a<0,得
a<-,即
a∈(-∞,-)…(8分)
(2)当
x=>0,即a>0时,
①若
e≤,则f'(x)≤0对x∈(0,e]成立,所以f(x)在区间(0,e]上单调递减,
所以,f(x)在区间(0,e]上的最小值为
f(e)=+alne=+a>0,
显然,f(x)在区间(0,e]上的最小值小于0不成立 …(10分)
②若
0<<e,即
a>时,则有
| x | (0,) | | (,e) |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
所以f(x)在区间(0,e]上的最小值为
f()=a+aln,
由
f()=a+aln=a(1-lna)<0,
得 1-lna<0,解得a>e,即a∈(e,+∞).
综上,由(1)(2)可知:
a∈(-∞,-)∪(e,+∞)符合题意.…(12分)
点评:本题考查函数的导数的应用,考查分类讨论思想的应用,同时考查转化思想的应用.



 优等生题库系列答案
优等生题库系列答案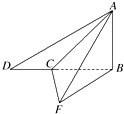 如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(
如图,为测量某建筑物AB的高度及取景点C与F之间的距离(点B,C,D,F 在同一水平面上,AB⊥平面BCF,且B,C,D三点共线),某校研究性学习小组的同学在C,D,F三点处测得顶点A的仰角分别为45°,30°,30°.若∠FCB=60°,CD=16(