
分析 把已知等式两边平方,利用完全平方公式及同角三角函数间的基本关系变形求出2sinαcosα的值,进而判断出sinα-cosα的正负,利用完全平方公式及同角三角函数间的基本关系求出sinα-cosα的值,联立求出sinα与cosα的值,即可确定出$\frac{1}{tanα}$的值.
解答 解:把sinα+cosα=$\frac{1}{5}$①,两边平方得:(sinα+cosα)2=1+2sinαcosα=$\frac{1}{25}$,
∴2sinαcosα=-$\frac{24}{25}$,
∵α∈(0,π),
∴sinα>0,cosα<0,即sinα-cosα>0,
∴(sinα-cosα)2=1-2sinαcosα=$\frac{49}{25}$,即sinα-cosα=$\frac{7}{5}$②,
联立①②,解得:sinα=$\frac{4}{5}$,cosα=-$\frac{3}{5}$,
则$\frac{1}{tanα}$=$\frac{cosα}{sinα}$=-$\frac{3}{4}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键,属于基础题.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
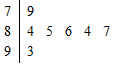 如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是巴蜀中学“高2017级跃动青春自编操”比赛上,七位评委为某班打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A. | 84,84 | B. | 84,85 | C. | 85,84 | D. | 85,85 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com