
(5分)已知椭圆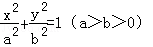 的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使
的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使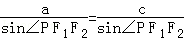 ,则该椭圆的离心率的取值范围为( )
,则该椭圆的离心率的取值范围为( )
A.(0, ) B.(
) B.(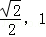 ) C.(0,
) C.(0,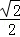 ) D.(
) D.( ,1)
,1)
D
【解析】
试题分析:由“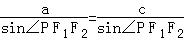 ”的结构特征,联想到在△PF1F2中运用由正弦定理得:
”的结构特征,联想到在△PF1F2中运用由正弦定理得: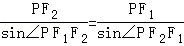 两者结合起来,可得到
两者结合起来,可得到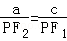 ,再由焦点半径公式,代入可得到:a(a+ex0)=c(a﹣ex0)解出x0,由椭圆的范围,建立关于离心率的不等式求解.要注意椭圆离心率的范围.
,再由焦点半径公式,代入可得到:a(a+ex0)=c(a﹣ex0)解出x0,由椭圆的范围,建立关于离心率的不等式求解.要注意椭圆离心率的范围.
【解析】
在△PF1F2中,由正弦定理得: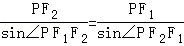
则由已知得: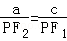 ,
,
即:aPF1=cPF2
设点P(x0,y0)由焦点半径公式,
得:PF1=a+ex0,PF2=a﹣ex0
则a(a+ex0)=c(a﹣ex0)
解得:x0=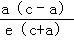 =
=
由椭圆的几何性质知:x0>﹣a则 >﹣a,
>﹣a,
整理得e2+2e﹣1>0,解得:e<﹣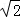 ﹣1或e>
﹣1或e>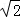 ﹣1,又e∈(0,1),
﹣1,又e∈(0,1),
故椭圆的离心率:e∈(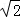 ﹣1,1),
﹣1,1),
故选D.


科目:高中数学 来源:[同步]2014年人教A版选修一1-2第四章4.2练习卷(解析版) 题型:选择题
如图是“集合”的知识结构图,如果要加入“子集”,则应放在( )
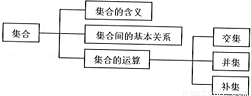
A.“集合的含义”的下位 B.“集合间的基本关系”的下位
C.“交集”的下位 D.“集合的运算”的下位
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•石家庄一模)登山族为了了解某山高y(km)与气温x(°C)之间的关系,随机统计了4次山高与相应的气温,并制作了对照表如下:
气温(0C) | 18 | 13 | 10 | ﹣1 |
|
山高 | (km) | 24 | 34 | 38 | 64 |
由表中数据,得到线性回归方程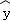 =﹣2x+
=﹣2x+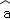 (
(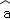 ∈R),由此估计山高为72km处气温的度数是( )
∈R),由此估计山高为72km处气温的度数是( )
A.﹣10 B.﹣8 C.﹣6 D.﹣4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:解答题
(12分)已知动圆M过定点F(0,﹣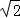 ),且与直线y=
),且与直线y=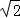 相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,
相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,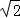 )在椭圆N上.
)在椭圆N上.
(1)求动圆圆心M的轨迹Γ的方程及椭圆N的方程;
(2)若动直线l与轨迹Γ在x=﹣4处的切线平行,且直线l与椭圆N交于B,C两点,试求当△ABC面积取到最大值时直线l的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)若方程Ax2+By2=1表示焦点在y轴上的双曲线,则A、B满足的条件是( )
A.A>0,且B>0 B.A>0,且B<0
C.A<0,且B>0 D.A<0,且B<0
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)设双曲线以椭圆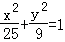 长轴上的两个端点为焦点,其一支上的动点到相应焦点的最短距离为5﹣2
长轴上的两个端点为焦点,其一支上的动点到相应焦点的最短距离为5﹣2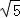 ,则双曲线的渐近线的斜率为( )
,则双曲线的渐近线的斜率为( )
A.±2 B.± C.±
C.±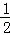 D.±
D.±
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
已知x、y、z∈R,且2x+3y+3z=1,则x2+y2+z2的最小值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]人教B版选修4-5 1.1不等式的性质和一元二次不等式的解法(解析版) 题型:选择题
(2014•宝山区一模)设a和b都是非零实数,则不等式a>b和
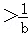 同时成立的充要条件是( )
同时成立的充要条件是( )
A.a>b B.a>b>0 C.a>0>b D.0>a>b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com