
已知x、y、z∈R,且2x+3y+3z=1,则x2+y2+z2的最小值为 .
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第四章4.2练习卷(解析版) 题型:选择题
如图是集合的知识结构图,如果要加入“全集”,则应该放在( )
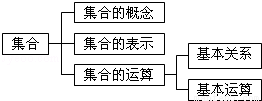
A.“集合的概念”的下位 B.“集合的表示”的下位
C.“基本关系”的下位 D.“基本运算”的下位
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•重庆)已知变量x与y正相关,且由观测数据算得样本平均数 =3,
=3,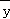 =3.5,则由该观测数据算得的线性回归方程可能是( )
=3.5,则由该观测数据算得的线性回归方程可能是( )
A.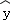 =0.4x+2.3 B.
=0.4x+2.3 B.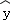 =2x﹣2.4 C.
=2x﹣2.4 C.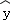 =﹣2x+9.5 D.
=﹣2x+9.5 D.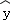 =﹣0.3x+4.4
=﹣0.3x+4.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)已知椭圆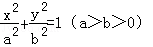 的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使
的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使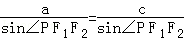 ,则该椭圆的离心率的取值范围为( )
,则该椭圆的离心率的取值范围为( )
A.(0, ) B.(
) B.(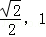 ) C.(0,
) C.(0,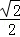 ) D.(
) D.( ,1)
,1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
若正数a、b、c、d满足ab+bc+cd+ad=1,那么a+b+c+d的最小值是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
(2012•怀化二模)已知a+b+c=1,m=a2+b2+c2,则m的最小值为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:选择题
已知实数x,y,z满足x+y+2z=1, ,则z的取值范围是( )
,则z的取值范围是( )
A. B.
B.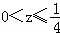 C.0≤z≤2 D.0<z≤1
C.0≤z≤2 D.0<z≤1
查看答案和解析>>
科目:高中数学 来源:2016届陕西省高一下学期期末考试数学试卷(解析版) 题型:选择题
已知函数f(x)=2sin(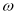 x+
x+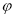 )(其中
)(其中 >0,∣
>0,∣ ∣<
∣<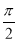 )的图像的相邻两条对称轴间的距离是
)的图像的相邻两条对称轴间的距离是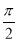 ,且f(0)=
,且f(0)=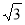 ,则
,则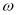 和
和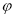 的值分别是( )
的值分别是( )
A.2,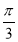 B.2,
B.2,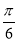 C.4,
C.4, 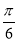 D.4,
D.4, 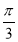
查看答案和解析>>
科目:高中数学 来源:[同步]人教B版选修4-5 1.1不等式的性质和一元二次不等式的解法(解析版) 题型:选择题
(2014•武汉模拟)一元二次不等式2kx2+kx﹣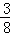 <0对一切实数x都成立,则k的取值范围是( )
<0对一切实数x都成立,则k的取值范围是( )
A.(﹣3,0) B.(﹣3,0] C.[﹣3,0] D.(﹣∞,﹣3)∪[0,+∞)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com