
(12分)已知动圆M过定点F(0,﹣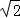 ),且与直线y=
),且与直线y=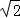 相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,
相切,椭圆N的对称轴为坐标轴,一个焦点为F,点A(1,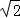 )在椭圆N上.
)在椭圆N上.
(1)求动圆圆心M的轨迹Γ的方程及椭圆N的方程;
(2)若动直线l与轨迹Γ在x=﹣4处的切线平行,且直线l与椭圆N交于B,C两点,试求当△ABC面积取到最大值时直线l的方程.
(1)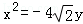 .
. ;(2)y=
;(2)y=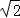 x±2.
x±2.
【解析】
试题分析:(1)由抛物线定义得,点M的轨迹是以F(0,﹣ )为焦点,直线y=
)为焦点,直线y= 为准线的抛物线,由此可得轨迹Γ的方程;设出椭圆方程,利用点A(1,
为准线的抛物线,由此可得轨迹Γ的方程;设出椭圆方程,利用点A(1, )在椭圆N上,可得椭圆N的方程;
)在椭圆N上,可得椭圆N的方程;
(2)设出切线方程,代入椭圆方程,求得|BC|,点A到直线的距离,表示出面积,利用基本不等式,即可求得△ABC面积取到最大值时直线l的方程.
【解析】
(1)过圆心M作直线y=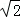 的垂线,垂足为H.
的垂线,垂足为H.
由题意得,|MH|=|MF|,由抛物线定义得,点M的轨迹是以F(0,﹣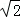 )为焦点,直线y=
)为焦点,直线y=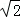 为准线的抛物线,
为准线的抛物线,
其方程为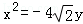 .
.
设椭圆方程为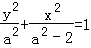 ,将点A代入方程
,将点A代入方程
整理得a4﹣5a2+4=0,解得a2=4或a2=1(舍去)
故所求的椭圆方程为 ;
;
(2)轨迹Γ的方程为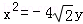 ,即
,即 ,则
,则 ,所以轨迹轨迹Γ在x=﹣4处的切线斜率为k=
,所以轨迹轨迹Γ在x=﹣4处的切线斜率为k= ,
,
设直线l方程为y= x+m,代入椭圆方程整理得4x2+2
x+m,代入椭圆方程整理得4x2+2 mx+m2﹣4=0
mx+m2﹣4=0
因为△=8m2﹣16(m2﹣4)>0,解得﹣2<m<2;
设B(x1,y1),C(x2,y2),则x1+x2=﹣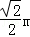 ,x1x2=
,x1x2=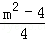
所以BC|= ×
× =
= ×
×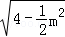
∵点A到直线的距离为d=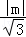 ,所以S△ABC=
,所以S△ABC= ×
×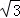 ×
×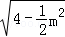 ×
×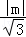 =
= ≤
≤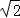
当且仅当 ,即m=±2时等号成立,此时直线l的方程为y=
,即m=±2时等号成立,此时直线l的方程为y=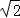 x±2.
x±2.


科目:高中数学 来源:[同步]2014年人教A版选修四4-1第一讲1.1练习卷(解析版) 题型:选择题
下列命题中正确的命题个数为( )
①如果一条直线与一平面平行,那么这条直线与平面内的任意直线平行;
②如果一条直线与一个平面相交,那么这条直线与这个平面内无数条直线垂直;
③过平面外一点有且只有一条直线与平面平行;
④一条直线上有两点到一个平面的距离相等,则这条直线平行于这个平面.
A.0 B.1 C.2 D.3
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.2练习卷(解析版) 题型:选择题
(2014•珠海二模)通过随机询问100名性别不同的小学生是否爱吃零食,得到如下的列联表:
| 男 | 女 | 总计 |
爱好 | 10 | 40 | 50 |
不爱好 | 20 | 30 | 50 |
总计 | 30 | 70 | 100 |
P(K2≥k) | 0.10 | 0.05 | 0.025 |
k | 2.706 | 3.841 | 50.24 |
由K2=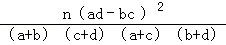 算得K2=
算得K2=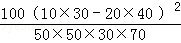 ≈4.762
≈4.762
参照附表,得到的正确结论( )
A.在犯错误的概率不超过5%的前提下,认为“是否爱吃零食与性别有关”
B.在犯错误的概率不超过5%的前提下,认为“是否爱吃零食与性别无关”
C.有97.5%以上的把握认为“是否爱吃零食与性别有关”
D.有97.5%以上的把握认为“是否爱吃零食与性别无关”
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•宜春模拟)在2013年9月15日,某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查,5家商场的售价x元和销售量y件之间的一组数据如下表所示:
价格x | 9 | 9.5 | 10 | 10.5 | 11 |
销售量y | 11 | 10 | 8 | 6 | 5 |
由散点图可知,销售量y与价格x之间有较好的线性相关关系,其线性回归方程是:y=﹣3.2x+a,则a=( )
A.﹣24 B.35.6 C.40.5 D.40
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修一1-2第一章1.1练习卷(解析版) 题型:选择题
(2014•重庆)已知变量x与y正相关,且由观测数据算得样本平均数 =3,
=3,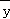 =3.5,则由该观测数据算得的线性回归方程可能是( )
=3.5,则由该观测数据算得的线性回归方程可能是( )
A.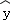 =0.4x+2.3 B.
=0.4x+2.3 B.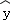 =2x﹣2.4 C.
=2x﹣2.4 C.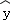 =﹣2x+9.5 D.
=﹣2x+9.5 D.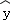 =﹣0.3x+4.4
=﹣0.3x+4.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:填空题
(5分)(2014•台州一模)双曲线x2﹣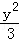 =1的两条渐近线方程为 .
=1的两条渐近线方程为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年人教A版选修2-1 第二章圆锥曲线与方程练习卷(解析版) 题型:选择题
(5分)已知椭圆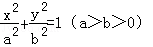 的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使
的左、右焦点分别为F1(﹣c,0),F2(c,0),若椭圆上存在点P使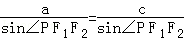 ,则该椭圆的离心率的取值范围为( )
,则该椭圆的离心率的取值范围为( )
A.(0, ) B.(
) B.(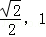 ) C.(0,
) C.(0,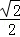 ) D.(
) D.( ,1)
,1)
查看答案和解析>>
科目:高中数学 来源:[同步]2014人教B版选修4-5 2.4最大值与最小值 优化数学模型(解析版) 题型:填空题
(2012•怀化二模)已知a+b+c=1,m=a2+b2+c2,则m的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com