Question

【题目】某公司在招聘员工时，要进行笔试，面试和实习三个过程．笔试设置了3个题，每一个题答对得5分，否则得0分．面试则要求应聘者回答3个问题，每一个问题答对得5分，否则得0分．并且规定在笔试中至少得到10分，才有资格参加面试，而笔试和面试得分之和至少为25分，才有实习的机会．现有甲去该公司应聘，假设甲答对笔试中的每一个题的概率为，答对面试中的每一个问题的概率为．

（1）求甲获得实习机会的概率；

（2）设甲在去应聘过程中的所得分数为随机变量，求的分布列和数学期望．

Answer 1

【答案】（1）；（2）分布列见解析，

【解析】

（1）笔试和面试得分之和为25分的情况为：笔试和面试得分分别为10，15；或15，10．利用相互独立与互斥事件概率计算公式即可得出．笔试和面试得分之和为30分的情况为：笔试和面试得分都为15．利用相互独立与互斥事件概率计算公式即可得出．

（2）的取值为0，5，10，15，20，25，30，对笔试和面试得分情况分类讨论，分别利用相互独立与互斥事件概率计算公式即可得出．

（1）笔试和面试得分之和为25分的概率为．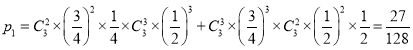

笔试和面试得分之和为30分的概率为．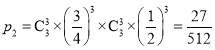

∴甲获得实习机会的概率．

（2）的取值为0，5，10，15，20，25，30，

，，，

．

．

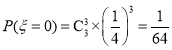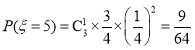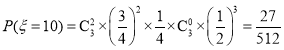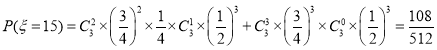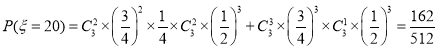由（1）可知：笔试和面试得分之和为25分的概率．

笔试和面试得分之和为30分的概率．

∴

．