考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(I)f′(x)=x2+2ax-3a2=(x+3a)(x-a)(a>0).由a>0,可知a>-3a.分别解出f′(x)>0,f′(x)<0,即可得出函数的单调区间.
(II)对任意实数x1,x2∈(-∞,a),不等式f(x1)<g(x2)恒成立?x∈(-∞,a),f(x)max<g(x)min.分别利用导数和二次函数研究其单调性极值最值即可.
解答:
解:(I)f′(x)=x2+2ax-3a2=(x+3a)(x-a)(a>0).
∵a>0,∴a>-3a.
令f′(x)>0,解得x>a或x<-3a;令f′(x)<0,解得-3a<x<a.
∴f(x)的单调递增区间为(-∞,-3a),(a,+∞);f(x)的单调递减区间为(-3a,a).
(II)对任意实数x1,x2∈(-∞,a),不等式f(x1)<g(x2)恒成立?x∈(-∞,a),f(x)max<g(x)min.
由(I)可知:f(x)在区间(-∞,-3a)单调递增;在区间(-3a,a)上单调递减.
∴f(x)max=f(-3a)=-9a3+9a3+9a3+2a-1=9a3+2a-1.
g(x)=(x+2)2+9a3+3≥9a3+3,∴当x=-2时,g(x)min=9a3+3.
∴9a3+2a-1≤9a2+3,又a>0,解得0<a≤2.
∴a的取值范围是(0,2].
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性,考查了恒成立问题的等价转化方法,考查了推理能力和计算能力,属于难题.



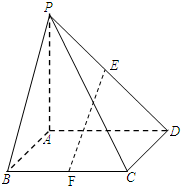 在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.
在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD,点E、F分别是PD、BC的中点.