
【题目】已知二次函数![]() .
.
(1)若![]() 是
是![]() 的两个不同零点,是否存在实数
的两个不同零点,是否存在实数![]() ,使
,使![]() 成立?若存在,求
成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(2)设![]() ,函数
,函数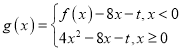 ,存在
,存在![]() 个零点.
个零点.
(i)求![]() 的取值范围;
的取值范围;
(ii)设![]() 分别是这
分别是这![]() 个零点中的最小值与最大值,求
个零点中的最小值与最大值,求![]() 的最大值.
的最大值.
【答案】(1) 不存在.理由见解析;
(2) (i) ![]() (ii)
(ii) ![]()
【解析】
(1) .假设存在实数![]() 满足题意,由韦达定理可得:
满足题意,由韦达定理可得:![]()
![]() ,解得
,解得![]() ,又
,又![]() ,即
,即![]() ,综合可得假设不成立;
,综合可得假设不成立;
(2) (i)作出函数![]() 的图象,观察图像即可求出
的图象,观察图像即可求出![]() 的取值范围;
的取值范围;
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .即
.即![]() ,因为
,因为![]()
![]() ,代入运算可得解.
,代入运算可得解.
解:(1)依题意可知,![]() .假设存在实数
.假设存在实数![]() ,使
,使![]() 成立.
成立.
因为![]() 有两个不同零点,.
有两个不同零点,.
所以![]() ,解得
,解得![]() .
.
由韦达定理得![]()
所以![]()
![]()
解得![]() ,而
,而![]() ,故不存在.
,故不存在.
(2)因为![]() ,设
,设![]() ,则
,则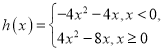 ,
,
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
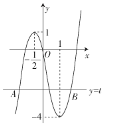
(i)作出函数![]() 的图象,如图所示,所以
的图象,如图所示,所以![]() .
.
(ii)设直线![]() 与此图象的最左边和最右边的交点分别为
与此图象的最左边和最右边的交点分别为![]() .
.
由![]() ,得
,得![]()
由![]() ,得
,得![]()
所以![]()
因为![]()
![]() ,
,
所以当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
故![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】从![]() 年
年![]() 月份,某市街头出现共享单车,到
月份,某市街头出现共享单车,到![]() 月份,根据统计,市区所有人骑行过共享单车的人数已占
月份,根据统计,市区所有人骑行过共享单车的人数已占![]() ,骑行过共享单车的人数中,有
,骑行过共享单车的人数中,有![]() 是大学生(含大中专及高职),该市区人口按
是大学生(含大中专及高职),该市区人口按![]() 万计算,大学生人数约
万计算,大学生人数约![]() 万人.
万人.
(1)任选出一名大学生,求他(她)骑行过共享单车的概率;
(2)随单车投放数量增加,乱停乱放成为城市管理的问题,以下是累计投放单车数量![]() 与乱停乱放单车数量
与乱停乱放单车数量![]() 之间的关系图表:
之间的关系图表:
累计投放单车数量 |
|
|
|
|
|
乱停乱放单车数量 |
|
|
|
|
|
①计算![]() 关于
关于![]() 的线性回归方程(其中
的线性回归方程(其中![]() 精确到
精确到![]() 值保留三位有效数字),并预测当
值保留三位有效数字),并预测当![]() 时,单车乱停乱放的数量;
时,单车乱停乱放的数量;
②已知该市共有五个区,其中有两个区的单车乱停乱放数量超过标准.在“双创”活动中,检查组随机抽取三个区调查单车乱停乱放数量, ![]() 表示“单车乱停乱放数量超过标准的区的个数”,求
表示“单车乱停乱放数量超过标准的区的个数”,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
参考公式和数据:回归直线方程![]() 中的斜率和截距的最小二乘法估计公式分别为
中的斜率和截距的最小二乘法估计公式分别为
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求![]() 和
和![]() 的直角坐标方程;
的直角坐标方程;
(2)若曲线![]() 截直线
截直线![]() 所得线段的中点坐标为
所得线段的中点坐标为![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为![]() =0.85x-85.71,则下列结论中不正确的是
=0.85x-85.71,则下列结论中不正确的是
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(![]() ,
,![]() )
)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重比为58.79kg
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进入12月以业,在华北地区连续出现两次重污染天气的严峻形势下,我省坚持保民生,保蓝天,各地严格落实机动车限行等一系列“管控令”,某市交通管理部门为了了解市民对“单双号限行”的态度,随机采访了200名市民,将他们的意见和是否拥有私家车的情况进行了统计,得到如下的![]() 列联表:
列联表:
赞同限行 | 不赞同限行 | 合计 | |
没有私家车 | 90 | 20 | 110 |
有私家车 | 70 | 40 | 110 |
合计 | 160 | 60 | 220 |
(1)根据上面的列联表判断能否在犯错误的概率不超过![]() 的前提下认为“对限行的态度与是否拥有私家车有关”;
的前提下认为“对限行的态度与是否拥有私家车有关”;
(2)为了了解限行之后是否对交通拥堵、环境染污起到改善作用,从上述调查的不赞同限行的人员中按是否拥有私家车分层抽样抽取6人,再从这6人中随机抽出3名进行电话回访,求3人中至少有1人没有私家车的概率.
附: 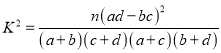 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】技术员小张对甲、乙两项工作投入时间![]() (小时)与做这两项工作所得报酬
(小时)与做这两项工作所得报酬![]() (百元)的关系式为:
(百元)的关系式为:![]() ,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
,若这两项工作投入的总时间为120小时,且每项工作至少投入20小时.
(1)试建立小张所得总报酬![]() (单位:百元)与对乙项工作投入的时间
(单位:百元)与对乙项工作投入的时间![]() (单位:小时)的函数关系式,并指明函数定义域;
(单位:小时)的函数关系式,并指明函数定义域;
(2)小张如何计划使用时间,才能使所得报酬最高?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是:( )
①设函数![]() 可导,则
可导,则![]() ;
;
②过曲线![]() 外一定点做该曲线的切线有且只有一条;
外一定点做该曲线的切线有且只有一条;
③已知做匀加速运动的物体的运动方程是![]() 米,则该物体在时刻
米,则该物体在时刻![]() 秒的瞬时速度是
秒的瞬时速度是![]() 米
米![]() 秒;
秒;
④一物体以速度![]() (米/秒)做直线运动,则它在
(米/秒)做直线运动,则它在![]() 到
到![]() 秒时间段内的位移为
秒时间段内的位移为![]() 米;
米;
⑤已知可导函数![]() ,对于任意
,对于任意![]() 时,
时,![]() 是函数
是函数![]() 在
在![]() 上单调递增的充要条件.
上单调递增的充要条件.
A. ①③B. ③④C. ②③⑤D. ③⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了了解学生对电子竞技的兴趣,从该校高二年级的学生中随机抽取了![]() 人进行检查,已知这
人进行检查,已知这![]() 人中有
人中有![]() 名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有
名男生对电子竞技有兴趣,而对电子竞技没兴趣的学生人数与电子竞技竞技有兴趣的女生人数一样多,且女生中有![]() 的人对电子竞技有兴趣.
的人对电子竞技有兴趣.
![]() 在被抽取的女生中与
在被抽取的女生中与![]() 名高二
名高二![]() 班的学生,其中有
班的学生,其中有![]() 名女生对电子产品竞技有兴趣,先从这
名女生对电子产品竞技有兴趣,先从这![]() 名学生中随机抽取
名学生中随机抽取![]() 人,求其中至少有
人,求其中至少有![]() 人对电子竞技有兴趣的概率;
人对电子竞技有兴趣的概率;
![]() 完成下面的
完成下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为“电子竞技的兴趣与性别有关”.
的把握认为“电子竞技的兴趣与性别有关”.
有兴趣 | 没兴趣 | 合计 | |
男生 | |||
女生 | |||
合计 |
参考数据:
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
参考公式:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com