
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() 是
是![]() 边上异于端点的动点,
边上异于端点的动点,![]() 于点
于点![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠至
折叠至![]() 处,使面
处,使面![]() 面
面![]() .点
.点![]() 分别为
分别为![]() 的中点.
的中点.
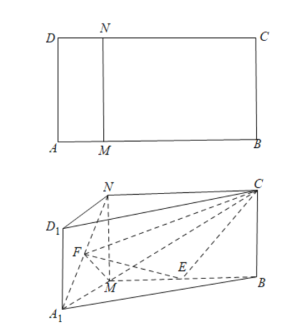
(1)证明:![]() //面
//面![]() ;
;
(2)设![]() ,当x为何值时,四面体
,当x为何值时,四面体![]() 的体积最大,并求出最大值.
的体积最大,并求出最大值.
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 、
、![]() 分别是离心率
分别是离心率![]() 的椭圆
的椭圆![]() 的左右项点,P是椭圆E的上顶点,且
的左右项点,P是椭圆E的上顶点,且![]() .
.
(1)求椭圆E的方程;
(2)若动直线![]() 过点
过点![]() ,且与椭圆E交于A、B两点,点M与点B关于y轴对称,求证:直线
,且与椭圆E交于A、B两点,点M与点B关于y轴对称,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着网络的普及,数码产品早已走进千家万户的生活,为了节约资源,促进资源循环利用,折旧产品回收行业得到迅猛发展,电脑使用时间越长,回收价值越低,某二手电脑交易市场对2018年回收的折旧电脑交易前使用的时间进行了统计,得到如图所示的频率分布直方图,在如图对时间使用的分组中,将使用时间落入各组的频率视为概率.
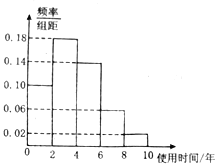
(1)若在该市场随机选取1个2018年成交的二手电脑,求其使用时间在![]() 上的概率;
上的概率;
(2)根据电脑交易市场往年的数据,得到如图所示的散点图及一些统计量的值,其中![]() (单位:年)表示折旧电脑的使用时间,
(单位:年)表示折旧电脑的使用时间,![]() (单位:百元)表示相应的折旧电脑的平均交易价格.
(单位:百元)表示相应的折旧电脑的平均交易价格.
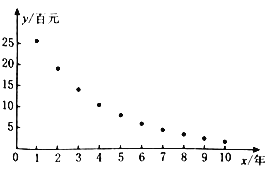
由散点图判断,可采用![]() 作为该交易市场折旧电脑平均交易价格与使用年限
作为该交易市场折旧电脑平均交易价格与使用年限![]() 的回归方程,若
的回归方程,若![]() ,
,![]() ,选用如下参考数据,求
,选用如下参考数据,求![]() 关于
关于![]() 的回归方程,并预测在区间
的回归方程,并预测在区间![]() (用时间组的区间中点值代表该组的值)上折旧电脑的价格.
(用时间组的区间中点值代表该组的值)上折旧电脑的价格.
|
|
|
|
|
|
5.5 | 8.5 | 1.9 | 301.4 | 79.75 | 385 |
附:参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: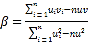 ,
,![]() .参考数据:
.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据《环境空气质量指数![]() 技术规定(试行)》规定:空气质量指数在区间
技术规定(试行)》规定:空气质量指数在区间![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数
时,其对应的空气质量状况分别为优、良、轻度污染、中度污染、重度污染、严重污染.如图为某市2019年10月1日至10月7日的空气质量指数![]() 直方图,在这7天内,下列结论正确的是( )
直方图,在这7天内,下列结论正确的是( )
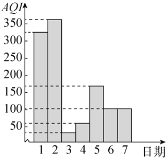
A.前4天![]() 的方差小于后3天
的方差小于后3天![]() 的方差
的方差
B.这7天内空气质量状况为严重污染的天数为3
C.这7天的平均空气质量状况为良
D.空气质量状况为优或良的概率为![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
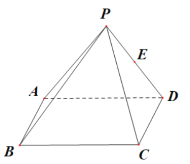
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形,![]() ,侧面
,侧面![]() 为等边三角形且垂直于底面
为等边三角形且垂直于底面![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)在棱![]() 上取一点
上取一点![]() 使直线
使直线![]() ∥平面
∥平面![]() 并证明;
并证明;
(2)在(1)的条件下,当棱![]() 上存在一点
上存在一点![]() ,使得直线
,使得直线![]() 与底面
与底面![]() 所成角为
所成角为![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《孙子算经》是中国古代重要的数学著作.其中的一道题“今有木,方三尺,高三尺,欲方五寸作枕一枚.问:得几何?”意思是:“有一块棱长为3尺的正方体方木,要把它作成边长为5寸的正方体枕头,可作多少个?”现有这样的一个正方体木料,其外周已涂上油漆,则从切割后的正方体枕头中任取一块,恰有一面涂上油漆的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),将曲线
为参数),将曲线![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() ,在以原点为极点,
,在以原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)说明曲线![]() 是哪一种曲线,并将曲线
是哪一种曲线,并将曲线![]() 的方程化为极坐标方程;
的方程化为极坐标方程;
(2)已知点![]() 是曲线
是曲线![]() 上的任意一点,求点
上的任意一点,求点![]() 到直线
到直线![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
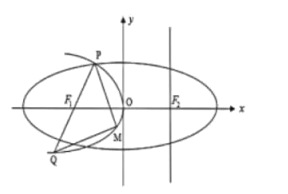
【题目】如图,设抛物线C1:![]() 的准线1与x轴交于椭圆C2:
的准线1与x轴交于椭圆C2:![]() 的右焦点F2,F1为C2的左焦点.椭圆的离心率为
的右焦点F2,F1为C2的左焦点.椭圆的离心率为![]() ,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
,抛物线C1与椭圆C2交于x轴上方一点P,连接PF1并延长其交C1于点Q,M为C1上一动点,且在P,Q之间移动.
(1)当![]() 取最小值时,求C1和C2的方程;
取最小值时,求C1和C2的方程;
(2)若△PF1F2的边长恰好是三个连续的自然数,当△MPQ面积取最大值时,求面积最大值以及此时直线MP的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com