
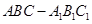 中,侧棱
中,侧棱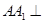 底面
底面 ,
,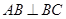 ,
,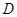 为
为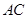 的中点,
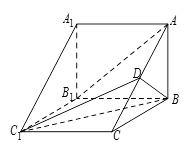
的中点,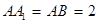 .
.
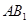 //平面
//平面 ;
;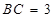 ,求四棱锥
,求四棱锥 的体积.
的体积.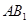 //平面
//平面 ,需要在平面
,需要在平面 内找一条与
内找一条与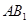 平行的直线,而要找这条直线一般通过作过
平行的直线,而要找这条直线一般通过作过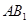 且与平面
且与平面 相交的平面来找.在本题中联系到
相交的平面来找.在本题中联系到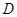 为
为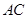 中点,故连结
中点,故连结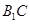 ,这样便得一平面
,这样便得一平面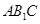 ,接下来只需证
,接下来只需证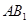 与平面
与平面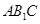 和平面
和平面 的交线平行即可.
的交线平行即可. 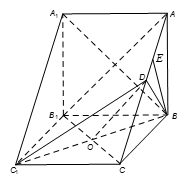
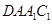 为一直角梯形,故易得其面积,本题的关键是求出点B到平面
为一直角梯形,故易得其面积,本题的关键是求出点B到平面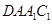 的距离.由于
的距离.由于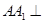 平面
平面 ,所以易得平面
,所以易得平面
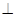 平面
平面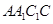 .平面
.平面
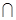 平面
平面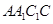
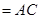 .根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面
.根据两平面垂直的性质定理知,只需过B作交线AC的垂线即可得点B到平面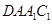 的距离,从而求出体积.
的距离,从而求出体积.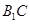 ,设
,设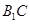 与
与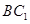 相交于点
相交于点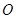 ,连接
,连接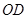 ,
,
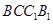 是平行四边形,
是平行四边形,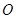 为
为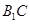 的中点.
的中点.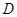 为
为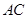 的中点,∴
的中点,∴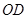 为△
为△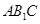 的中位线,
的中位线,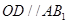 .
.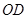
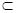 平面
平面 ,
,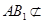 平面
平面 ,
,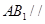 平面
平面 . 6分
. 6分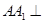 平面
平面 ,
,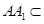 平面
平面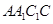 ,
,
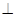 平面
平面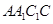 ,且平面
,且平面
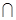 平面
平面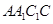
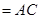 .
.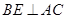 ,垂足为
,垂足为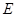 ,则
,则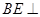 平面
平面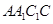 ,
, 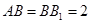 ,
,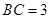 ,
, 中,
中,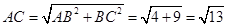 ,
,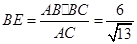 ,
,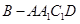 的体积
的体积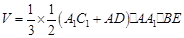
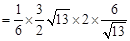
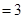 12分
12分

 新编小学单元自测题系列答案
新编小学单元自测题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com