Question

13．已知圆M过两点A（1，-1），B（-1，1），且圆心M在直线x+y-2=0上．
（1）求圆M的方程．
（2）设P是直线3x+4y+8=0上的动点，PC、PD是圆M的两条切线，C、D为切点，求四边形PCMD面积的最小值．

Answer 1

分析 （1）设圆心M（a，b），依题意，可求得AB的垂直平分线l的方程，利用方程组可求得直线l与直线x+y-2=0的交点，即圆心M（a，b），再求得r=|MA|=2，即可求得
圆M的方程；
（2）作出图形，易得S_PCMD=|MC|•|PC|=2$\sqrt{|PM{|}^{2}-|MC{|}^{2}}$=2$\sqrt{|PM{|}^{2}-4}$，利用点到直线间的距离公式可求得|PM|_min=d=3，从而可得（S_PCMD）_min=2$\sqrt{5}$．

解答 解：（1）设圆心M（a，b），则a+b-2=0①，
又A（1，-1），B（-1，1），
∴k_AB=$\frac{1-（-1）}{-1-1}$=-1，
∴AB的垂直平分线l的斜率k=1，又AB的中点为O（0，0），
∴l的方程为y=x，而直线l与直线x+y-2=0的交点就是圆心M（a，b），
由$\left\{\begin{array}{l}a+b-2=0\\ a=b\end{array}\right.$解得：$\left\{\begin{array}{l}a=1\\ b=1\end{array}\right.$，又r=|MA|=2，
∴圆M的方程为（x-1）²+（y-1）²=4．
（2）如图：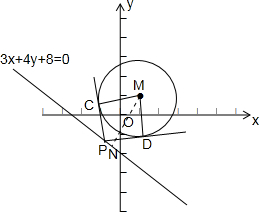

S_PCMD=|MC|•|PC|=2$\sqrt{|PM{|}^{2}-|MC{|}^{2}}$=2$\sqrt{|PM{|}^{2}-4}$，
又点M（1，1）到3x+4y+8=0的距离d=|MN|=$\frac{|3×1+4×1+8|}{\sqrt{{3}^{2}+{4}^{2}}}$=3，
所以|PM|_min=d=3，
所以（S_PCMD）_min=2$\sqrt{{3}^{2}-4}$=2$\sqrt{5}$．

点评 本题考查直线和圆的方程的应用，着重考查圆的标准方程及点到直线间的距离公式的应用，考查转化思想与作图、运算及求解能力，属于中档题．