
 如图,在棱长都相等的四面体ABCD中,点E是棱AD的中点.
如图,在棱长都相等的四面体ABCD中,点E是棱AD的中点.分析 (1)根据已知条件,四面体ABCD为正四面体,设△BCD的中心为O,从而OA⊥底面BCD,过O作FG∥BC,连接DO并延长交BC于H,从而可以说明OH,OG,OA三直线两两垂直,从而分别以这三直线为x,y,z轴,建立空间直角坐标系,根据已知条件可求出图形上一些点的坐标.连接AH,可以说明∠AHO为侧面ABC与底面BCD所成角为α,并且可求出OA,OH,从而求得tanα;
(2)先说明OA为平面BCD的法向量,从而根据sin$β=|cos<\overrightarrow{OA},\overrightarrow{CE}>|=\frac{|\overrightarrow{OA}•\overrightarrow{CE}|}{|\overrightarrow{OA}||\overrightarrow{CE}|}$求出sinβ,从而求得cosβ;
(3)先假设存在点F,使直线AF与CE所成角为90°,可以设F($\frac{\sqrt{3}}{3},{y}_{0},0$),而若使直线AF与CE所成角为90°,从而AF⊥CE,从而根据$\overrightarrow{AF}•\overrightarrow{CE}=0$求出y0,从而确定F点的位置.
解答 解:(1)四面体ABCD的棱长都相等;
∴该四面体为正四面体;
∴A在底面BCD的投影为底面BCD的中心;设△BCD的中心为O,过O作BC的平行线,分别交BD,CD于F,G,连接DO并延长,交BC于H,则:H为BC中点;
∴OG⊥BC,OG⊥OE;
连接AO,则AO⊥底面BCD;
∴OH,OG,OA三直线两两垂直,∴分别以这三条直线为x,y,z轴,建立如图所示空间直角坐标系,设该正四面体棱长为2,则: A(0,0,$\frac{2\sqrt{6}}{3}$),B($\frac{\sqrt{3}}{3},-1,0$),C($\frac{\sqrt{3}}{3},1,0$),D($-\frac{2\sqrt{3}}{3},0,0$),H($\frac{\sqrt{3}}{3},0,0$),E($-\frac{\sqrt{3}}{3},0,\frac{\sqrt{6}}{3}$);
A(0,0,$\frac{2\sqrt{6}}{3}$),B($\frac{\sqrt{3}}{3},-1,0$),C($\frac{\sqrt{3}}{3},1,0$),D($-\frac{2\sqrt{3}}{3},0,0$),H($\frac{\sqrt{3}}{3},0,0$),E($-\frac{\sqrt{3}}{3},0,\frac{\sqrt{6}}{3}$);
连接AH,显然∠AHD为侧面ABC与底面BCD所成二面角的平面角;
且$OH=\frac{\sqrt{3}}{3},OA=\frac{2\sqrt{6}}{3}$;
∴$tanα=\frac{OA}{OH}=2\sqrt{2}$;
(2)显然$\overrightarrow{OA}=(0,0,\frac{2\sqrt{6}}{3})$为底面BCD的法向量;
$\overrightarrow{CE}=(-\frac{2\sqrt{3}}{3},-1,\frac{\sqrt{6}}{3})$;
∴$sinβ=|cos<\overrightarrow{OA},\overrightarrow{CE}>|$=$\frac{\frac{4}{3}}{\frac{2\sqrt{6}}{3}•\sqrt{3}}=\frac{\sqrt{2}}{3}$;
∴$cosβ=\frac{\sqrt{7}}{3}$;
(3)假设在直线BC上存在点F,使直线AF与CE所成角为90°,设F($\frac{\sqrt{3}}{3},{y}_{0},0$),则:
$\overrightarrow{AF}=(\frac{\sqrt{3}}{3},{y}_{0},-\frac{2\sqrt{6}}{3})$;
直线AF与CE所成角为90°,即AF⊥CE;
∴$\overrightarrow{AF}•\overrightarrow{CE}=-2-{y}_{0}-4=0$;
∴y0=-6;
∴存在点F,使直线AF与CE所成角为90°,并且F点在CB延长线上,且FB=5.
点评 考查正四面体的定义,等边三角形的中心也是重心,重心的性质:重心到顶点距离是它到对边中点距离的2倍,以及通过建立空间直角坐标系,利用空间向量解决线面角,异面直线的垂直等问题的方法,能确定空间点的坐标,二面角的平面角的定义,平面法向量的概念,直线与平面所成角和直线和平面法向量所成角的关系,三角函数的定义,向量垂直的充要条件.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{6}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
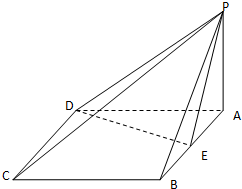 如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com