
| A. | $({\frac{5}{12},\frac{3}{4}}]$ | B. | $[{\frac{5}{12},+∞})$ | C. | $({0,\frac{5}{12}}]$ | D. | $({\frac{1}{3},\frac{1}{4}}]$ |
分析 先确定曲线的性质,然后结合图形确定临界状态,结合直线与圆相交的性质,可解得k的取值范围.
解答  解:y=$\sqrt{4-{x^2}}$+1可化为x2+(y-1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.
解:y=$\sqrt{4-{x^2}}$+1可化为x2+(y-1)2=4,y≥1,所以曲线为以(0,1)为圆心,2为半径的圆y≥1的部分.
直线y=k(x-2)+4过定点p(2,4),由图知,当直线经过A(-2,1)点时恰与曲线有两个交点,顺时针旋转到与曲线相切时交点变为一个.
且kAP=$\frac{4-1}{2+2}$=$\frac{34}{\;}$,由直线与圆相切得d=$\frac{|-1+4-2k|}{\sqrt{{k}^{2}+1}}$=2,
解得k=$\frac{5}{12}$,
则实数k的取值范围为($\frac{5}{12}$,$\frac{3}{4}$].
故选A.
点评 本题考查直线与圆相交的性质,同时考查了学生数形结合的能力,是个基础题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
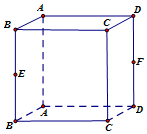 如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
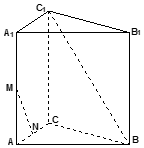 在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.
在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB=AC=AA1,∠CAB=90°,M、N分别是AA1和AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日最高气温t(单位:℃) | t≤22℃ | 22℃<t≤28℃ | 28℃<t≤32℃ | t>32℃ |
| 天数 | 6 | 12 | X | Y |
| 高温天气 | 非高温天气 | 合计 | |
| 旺销 | 2 | 22 | 24 |
| 不旺销 | 4 | 2 | 6 |
| 合计 | 6 | 24 | 30 |
| P(K2≥k) | 0.10 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com