
| A. | -2 | B. | 2 | C. | -4 | D. | 4 |
分析 设出直线方程,与抛物线方程联立,利用韦达定理,结合NA⊥NB,得到方程,即可求出p的值.
解答 解:设直线方程为y=2(x-$\frac{p}{2}$),A(x1,y1)、B(x2,y2),
代入抛物线方程,整理得4x2-6px+p2=0,
∴x1+x2=$\frac{3}{2}$p,x1x2=$\frac{1}{4}$p2,
由NA⊥NB,
得(x1+2,y1-2)•(x2+2,y2-2)=(x1+2)(x2+2)+[2(x1-$\frac{p}{2}$)-2][2(x2-$\frac{p}{2}$)-2]=0,
代入整理得3p2-4p-32=0,
∵p>0,∴解得p=4.
故选D.
点评 本题考查直线与抛物线位置关系的运用,考查韦达定理,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
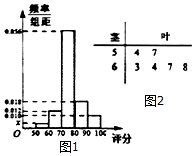 某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.
某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
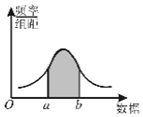
| A. | 组距越大,频率分布折线图越接近于它 | |
| B. | 样本容量越小,频率分布折线图越接近于它 | |
| C. | 阴影部分的面积代表总体在(a,b)内取值的百分比 | |
| D. | 阴影部分的平均高度代表总体在(a,b)内取值的百分比 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | 2 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | (-1)n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
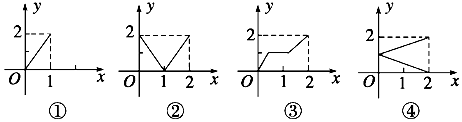
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com