
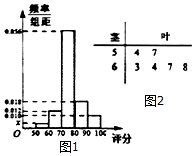
 ij��λΪ�˽�ס��������ŶԱ���λְ���ķ���������������50��ְ������֪50��ְ���Լס��������ŵ����ֶ�������[50��100]�ڣ�����50��ְ���Լײ��ŵ����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ���Լ�����50��ְ�����Ҳ�������������[50��60����[60��70���ڵ��������ݻ��Ƶľ�Ҷͼ����ͼ��ʾ��
ij��λΪ�˽�ס��������ŶԱ���λְ���ķ���������������50��ְ������֪50��ְ���Լס��������ŵ����ֶ�������[50��100]�ڣ�����50��ְ���Լײ��ŵ����ֻ��Ƶ�Ƶ�ʷֲ�ֱ��ͼ���Լ�����50��ְ�����Ҳ�������������[50��60����[60��70���ڵ��������ݻ��Ƶľ�Ҷͼ����ͼ��ʾ������ ��1�����ݸ���֮����1�����x��ֵ���ɣ�
��2���ֱ�����ס��������ŷ������������ȣ��Ƚϼ��ɣ�
��3����������ȡ�����������ݵ����л����¼��������������1��������������[50��60���ڵĻ����¼���������������ĸ��ʼ��ɣ�
��� �⣺��1��������ã���֪10x+0.012��10+0.056��10+0.018��10+0.010��10=1��
��ã�x=0.004��
��2���ײ��ŷ�������������Ϊ��
0.056��10+0.018��10+0.010��10=0.84��
�Ҳ��ŷ�������������Ϊ��1-$\frac{6}{50}$=0.88��
���Ҳ��ŷ������������Ƚϸߣ�
��3�������⣬���Ҳ��ŵ÷�Ϊ[50��60����[60��70����6���������ݴ�С��������Ϊ��
A1��A2��B1��B2��B3��B4��
�������ȡ�����������ݵ����л����¼��У�
{A1��A2}��{A1��B1}��{A1��B2}��{A1��B3}��{A1��B4}��
{A2��B1}��{A2��B2}��{A2��B3}��{A2��B4}��{B1��B2}��
{B1��B3}��{B1��B4}��{B2��B3}��{B2��B4}��{B3��B4}��
��15����
���С�������1��������������[50��60���ڡ�������
{A1��A2}��{A1��B1}��{A1��B2}��{A1��B3}��{A1��B4}��
{A2��B1}��{A2��B2}��{A2��B3}��{A2��B4}��9�������¼���
��������1��������������[50��60���ڵĸ���Ϊp=$\frac{9}{15}$=$\frac{3}{5}$��
���� ���⿼����Ƶ�ʷֱ�ֱ��ͼ��������������⣬��һ���е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2 | B�� | 2 | C�� | -4 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com