
分析 由题意作函数f(x)=|ex-1|的图象,令m=f(x),由图求出m的范围,代入方程g(x)=-1化简,由条件和图象判断出方程的根的范围,由一元二次方程根的分布问题列出不等式,求出t的取值范围.
解答 解:由题意作函数f(x)=|ex-1|的图象: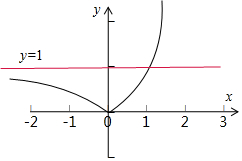
令m=f(x),由图得m≥0,
代入g(x)=f2(x)-tf(x)=-1得,
m2-tm=-1,即m2-tm+1=0,
∵满足g(x)=-1的x有三个,
∴由图得,即m2-tm+1=0有两个根,其中一个在(0,1)中,另外一个在[1,+∞)中,
∴$\left\{\begin{array}{l}{{0}^{2}-t×0+1>0}\\{{1}^{2}-t×1+1≤0}\\{△={t}^{2}-4>0}\end{array}\right.$,解得t>2,
即t的取值范围是(2,+∞),
故答案为:(2,+∞).
点评 本题考查方程根的个数问题的转化,一元二次方程根的分布问题,以及换元法的应用,考查数形结合思想,转化思想.


科目:高中数学 来源: 题型:选择题
| A. | ①④ | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 28 | C. | 40 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
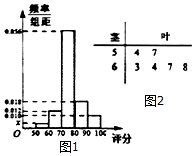 某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.
某单位为了解甲、乙两部门对本单位职工的服务情况,随机访问50名职工.已知50名职工对甲、乙两部门的评分都在区间[50,100]内,根据50名职工对甲部门的评分绘制的频率分布直方图,以及根据50名职工对乙部门评分中落在[50,60),[60,70)内的所有数据绘制的茎叶图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
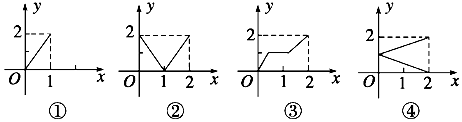
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com