
点P到平面四边形ABCD四条边的距离相等,则四边形ABCD是( )
A.某圆的内接四边形 B.某圆的外切四边形
C.正方形 D.任意四边形两个半圆
B
【解析】
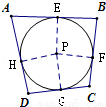
试题分析:过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H,以P为圆心、PE为半径作圆.根据切线的判定定理,证出四边形ABCD的各边所在直线都与圆P相切,得到四边形ABCD是圆P的外切四边形,从而得到答案.
【解析】
过P分别作AB、BC、CD、DA的垂线,垂足分别为E、F、G、H,
∵P到四边形ABCD四条边的距离相等,∴PE=PF=PG=PH.
以P为圆心,PE为半径作圆,如图所示.
∵直线AB经过点E,且AB⊥PE,∴直线AB与圆P相切.
∵PF=PE,∴点F在圆P上.
又∵直线BC经过点F,且BC⊥PF,∴直线BC与圆P相切.
同理可得直线CD、DA都与圆P相切.
由此可得四边形ABCD的各边都与圆P相切,即ABCD是圆P的外切四边形.
故选:B


科目:高中数学 来源:[同步]2015人教A版必修二2.1空间点、直线、平面间位置关系练习卷(解析版) 题型:
在三棱柱ABC﹣A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是( )
A.30° B.45° C.60° D.90°
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
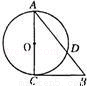
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AC为直径的圆交AB于D,则AD的长为( )
A.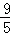 B.
B. C.
C.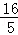 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
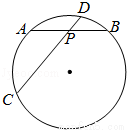
(2013•湖南)如图,在半径为 的⊙O中,弦AB,CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为 .
的⊙O中,弦AB,CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
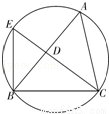
如图所示,圆的内接△ABC的∠C的平分线CD延长后交圆于点E,连接BE,已知BD=3,CE=7,BC=5,则线段BE=( )
A. B.
B.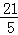 C.
C.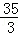 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
如图,A、B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
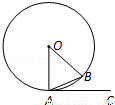
A.70° B.35° C.20° D.10°
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:填空题
若将复数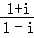 表示为a+bi(a,b∈R,i是虚数单位)的形式,则a+b= .
表示为a+bi(a,b∈R,i是虚数单位)的形式,则a+b= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
设a∈R,且(a+i)2i为正实数,则a=( )
A.2 B.1 C.0 D.﹣1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.2导数的运算练习卷(解析版) 题型:解答题
已知P(﹣1,1),Q(2,4)是曲线y=x2上的两点,求与直线PQ平行且与曲线相切的切线方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com