
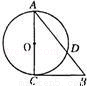
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AC为直径的圆交AB于D,则AD的长为( )
A.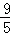 B.
B. C.
C.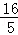 D.4
D.4
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:[同步]2015年人教A版必修二4.3 空间直角坐标系练习卷(解析版) 题型:
已知两点M1(﹣1,0,2),M2(0,3,﹣1),此两点间的距离为( )
A.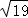 B.
B.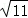 C.19 D.11
C.19 D.11
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-2 4.1变换的不变量 矩阵特征向量(解析版) 题型:填空题
已知矩阵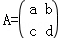 ,若矩阵A属于特征值3的一个特征向量为
,若矩阵A属于特征值3的一个特征向量为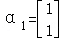 ,属于特征值﹣1的一个特征向量为
,属于特征值﹣1的一个特征向量为 ,则矩阵A= .
,则矩阵A= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:填空题
(2014•潮州二模)AB是圆O的直径,EF切圆O于C,AD⊥EF于D,AD=2,AB=6,则AC长为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
如图,AP为⊙O切线,P为切点,OA交⊙O于点B,∠A=40°,则∠APB=( )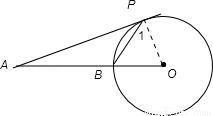
A.25° B.20° C.40° D.35°
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
(2005•福建)△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,则∠FDE与  ∠A的关系是( )
∠A的关系是( )
A.∠FDE+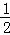 ∠A=90° B.∠FDE=
∠A=90° B.∠FDE=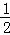 ∠A C.∠FDE+
∠A C.∠FDE+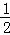 ∠A=180° D.无法确定
∠A=180° D.无法确定
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:填空题
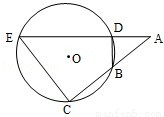
(2010•北京)如图,⊙O的弦ED,CB的延长线交于点A.若BD⊥AE,AB=4,BC=2,AD=3,则DE= ;CE= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.2圆内接四边形性质与判定定理(解析版) 题型:选择题
点P到平面四边形ABCD四条边的距离相等,则四边形ABCD是( )
A.某圆的内接四边形 B.某圆的外切四边形
C.正方形 D.任意四边形两个半圆
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:解答题
已知a,b,c是互不相等的实数,求证:由y=ax2+2bx+c,y=bx2+2cx+a,y=cx2+2ax+b确定的三条抛物线至少有一条与x轴有两个不同的交点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com