
已知a,b,c是互不相等的实数,求证:由y=ax2+2bx+c,y=bx2+2cx+a,y=cx2+2ax+b确定的三条抛物线至少有一条与x轴有两个不同的交点.
见解析
【解析】
试题分析:本题是一个至少性问题,可以利用反证法证明,其步骤为:①否定命题的结论,即假设“任何一条抛物线与x轴没有两个不同的交点”成立→②根据函数的性质可以得到三个函数对应方程的△≤0均成立→③利用不等式的性质,同向不等式求和→④得到的式子与实数的性质相矛盾→⑤故假设不成立,原结论成立.
【解析】
假设题设中的函数确定的三条抛物线都不与x有两个不同的交点
(即任何一条抛物线与x轴没有两个不同的交点),
由y=ax2+2bx+c,y=bx2+2cx+a,y=cx2+2ax+b得△1=(2b)2﹣4ac≤0,
△2=(2c)2﹣4ab≤0,
△3=(2a)2﹣4bc≤0.
同向不等式求和得,
4b2+4c2+4a2﹣4ac﹣4ab﹣4bc≤0,
∴2a2+2b2+2c2﹣2ab﹣2bc﹣2ac≤0,
∴(a﹣b)2+(b﹣c)2+(c﹣a)2≤0,
∴a=b=c,这与题设a,b,c互不相等矛盾,
因此假设不成立,从而命题得证.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源:[同步]2014新人教A版选修4-1 2.3圆的切线性质及判定定理练习(解析版) 题型:选择题
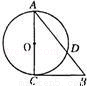
如图,Rt△ABC中,∠ACB=90°,AC=4,BC=3,以AC为直径的圆交AB于D,则AD的长为( )
A.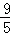 B.
B. C.
C.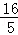 D.4
D.4
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:填空题
若将复数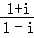 表示为a+bi(a,b∈R,i是虚数单位)的形式,则a+b= .
表示为a+bi(a,b∈R,i是虚数单位)的形式,则a+b= .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
设a∈R,且(a+i)2i为正实数,则a=( )
A.2 B.1 C.0 D.﹣1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-2 2.2直接证明与间接证明练习卷(解析版) 题型:填空题
若记号“*”表示求两个实数a与b的算术平均数的运算,即 ,则两边均含有运算符号“*”和“+”,且对于任意3个实数a、b、c都能成立的一个等式可以是 .
,则两边均含有运算符号“*”和“+”,且对于任意3个实数a、b、c都能成立的一个等式可以是 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:解答题
一艘轮船在航行中的燃料费和它的速度的立方成正比,已知在速度为每小时10公里时的燃料费是每小时6元,而其他与速度无关的费用是每小时96元,问此轮船以何种速度航行时,能使行驶每公里的费用总和最小?
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.2导数的运算练习卷(解析版) 题型:解答题
已知P(﹣1,1),Q(2,4)是曲线y=x2上的两点,求与直线PQ平行且与曲线相切的切线方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.4抛物线练习卷(解析版) 题型:填空题
已知F是抛物线y2=x的焦点,A、B是该抛物线上的两点,|AF|+|BF|=3,则线段AB的中点到y轴的距离为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com