
分析 (1)由已知求得$\overrightarrow{m}、\overrightarrow{n}$的坐标,结合$\overrightarrow m$∥$\overrightarrow n$列式化简求得曲线C的方程;
(2)联立直线方程与椭圆方程,化为(1+2k2)x2+4kx=0,再由弦长公式求得k,则直线方程可求.
解答 解:(Ⅰ)由已知$\overrightarrow m$=${\overrightarrow m_1}$+$\sqrt{2}$${\overrightarrow n_2}$=(0,x)+($\sqrt{2}{y}^{2}$,$\sqrt{2}$)=($\sqrt{2}{y}^{2}$,x+$\sqrt{2}$),
$\overrightarrow n$=${\overrightarrow m_2}$-$\sqrt{2}$${\overrightarrow n_1}$=(x,0)-($\sqrt{2}$,$\sqrt{2}$)=(x-$\sqrt{2}$,-$\sqrt{2}$),
∵$\overrightarrow m$∥$\overrightarrow n$,∴-2y2-(x+$\sqrt{2}$)(x-$\sqrt{2}$)=0.
即-2y2-x2+2=0.
∴所求曲线C的方程是:$\frac{{x}^{2}}{2}+{y}^{2}=1$;
(Ⅱ)联立$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,消去y得:(1+2k2)x2+4kx=0,
设M(x1,y1),N(x2,y2),则△=16k2≥0.
${x}_{1}+{x}_{2}=\frac{-4k}{1+2{k}^{2}}$.x1x2=0.
∴|MN|=$\sqrt{1+{k}^{2}}|{x}_{1}-{x}_{2}|=\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}•\sqrt{(\frac{-4k}{1+2{k}^{2}})^{2}}=\frac{4}{3}\sqrt{2}$,
解得:k=±1.
∴所求直线的方程为x-y+1=0或x+y-1=0.
点评 本题考查直线方程和曲线方程的求法,考查椭圆性质的应用,体现了“设而不求”的解题思想方法,是中档题.


 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x-y=0 | B. | $2x-y-\sqrt{2}=0$ | C. | $2x-3y-\sqrt{2}=0$ | D. | $x-y-\sqrt{2}=0$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
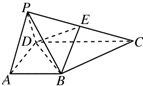 已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.
已知在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,2AB=2AD=CD,侧面PAD是正三角形且垂直于底面ABCD,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com