
| A. | 2x-y=0 | B. | $2x-y-\sqrt{2}=0$ | C. | $2x-3y-\sqrt{2}=0$ | D. | $x-y-\sqrt{2}=0$ |
分析 把双曲线的解析式变形后,根据题中的例子,两边对x求导且解出y′,把P的坐标代入求出切线的斜率,然后根据切点P的坐标和求出的斜率,写出切线方程即可.
解答 解:由双曲线${x^2}-\frac{y^2}{2}=1$,得到y2=2x2-2,
根据题意,两边同时对x求导得:2yy′=4x,解得y′=$\frac{2x}{y}$,
由$P({\sqrt{2},\sqrt{2}})$,得到过P得切线的斜率k=2,
则所求的切线方程为:y-$\sqrt{2}$=2(x-$\sqrt{2}$),即2x-y-$\sqrt{2}$=0.
故选:B.
点评 此题考查了求导法则的运用,以及根据一点和斜率会写出直线的方程.本题的类型是新定义题,此类题的作法是认真观察题中的例题,利用类比的方法求出所求的切线方程.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
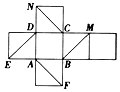 如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;
如图是正方体的平面展开图.关于这个正方体,有以下判断:①EC⊥平面AFN;| A. | ①③ | B. | ②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,-1) | B. | (1,-4) | C. | $({\frac{1}{9},-4})$ | D. | (9,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com