
分析 (1)△ABC绕BC旋转一周形成一个组合体,该组合体可看成圆锥CD中挖去一个小圆锥BD得到的.利用V几何体=V大圆锥-V小圆锥求解即可.
(2)取BC中点O,连接OE,OF,说明∠EOF即为AC与BD所成的角或其补角.推出∠EOF=60°或∠EOF=120°.然后求解即可.
解答 解:(1)如图,△ABC绕BC旋转一周形成一个组合体,该组合体可看成圆锥CD中挖去一个小圆锥BD得到的.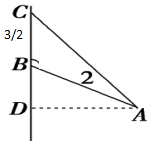
∵∠ABD=60°,AB=2,
∴AD=$\sqrt{3}$,BD=1.
∴V几何体=V大圆锥-V小圆锥
=$\frac{1}{3}$π•AD2•CD-$\frac{1}{3}$π•AD2•BD
=$\frac{1}{3}$π×($\sqrt{3}$)2×($\frac{3}{2}$+1-1)=$\frac{3}{2}$π.
(2)解:如图,取BC中点O,连接OE,OF,
∵OE∥AC,OF∥BD,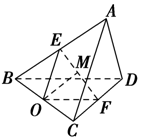
∴∠EOF即为AC与BD所成的角或其补角.
而AC,BD所成的角为60°,
∴∠EOF=60°或∠EOF=120°.
当∠EOF=60°时,EF=OE=OF=$\frac{1}{2}$;
当∠EOF=120°时,取EF中点M,则OM⊥EF,
EF=2EM=2OE•cos 30°=2×$\frac{\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$.
点评 本题考查空间几何体的体积以及点、线、面的距离的求法,考查空间想象能力以及计算能力.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
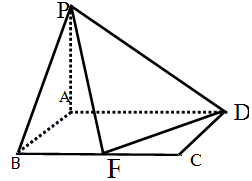 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=2,AB=1,F是线段BC的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin2x | B. | y=|cosx| | C. | y=-tanx | D. | $y=cos\frac{x}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com