
【题目】人最宝贵的是生命,然而有时候最不善待生命的恰恰是人类自己,在交通运输业发展迅猛的今天,由于不懂得交通法规,以及人们的交通安全观念和自我保护意识还没有跟上时代的步伐,那些在交通复杂多变的地方而引发的交通事故也是接连不断.为了警示市民,某市对近三年内某多发事故路口在每天![]() 时间段内发生的480次事故中随机抽取100次进行调研,数据按事发时间分成8组:
时间段内发生的480次事故中随机抽取100次进行调研,数据按事发时间分成8组:![]() (单位:小时),制成了如图所示的频率分布直方图.
(单位:小时),制成了如图所示的频率分布直方图.

(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这480次交通事故发生在时间段
的值,并根据频率分布直方图估计这480次交通事故发生在时间段![]() 与
与![]() 的次数;
的次数;
(Ⅱ)在抽出的100次交通事故中按时间段采用分层抽样的方法抽取10次进行个案分析,再从这10次交通事故中选取3次交通事故作重点专题研究.记这3次交通事故中发生时间在![]() 与
与![]() 的次数为
的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
科目:高中数学 来源: 题型:
【题目】已知定圆![]() ,动圆
,动圆![]() 过点
过点![]() 且与圆
且与圆![]() 相切,记圆心
相切,记圆心![]() 的轨迹为
的轨迹为![]() .
.
(I)求轨迹![]() 的方程;
的方程;
(Ⅱ)若与![]() 轴不重合的直线
轴不重合的直线![]() 过点
过点![]() ,且与轨迹
,且与轨迹![]() 交于
交于![]() 两点,问:在
两点,问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为定值?若存在,试求出点
为定值?若存在,试求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列4个命题:
①“若a、G、b成等比数列,则G2=ab”的逆命题;
②“如果x2+x﹣6≥0,则x>2”的否命题;
③在△ABC中,“若A>B”则“sinA>sinB”的逆否命题;
④当0≤α≤π时,若8x2﹣(8sinα)x+cos2α≥0对x∈R恒成立,则α的取值范围是0≤α≤![]() .
.
其中真命题的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
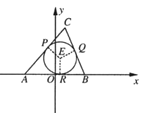
【题目】已知△ABC的两顶点坐标A(﹣1,0),B(1,0),圆E是△ABC的内切圆,在边AC,BC,AB上的切点分别为P,Q,R,|CP|=1(从圆外一点到圆的两条切线段长相等),动点C的轨迹为曲线M.
(I)求曲线M的方程;
(Ⅱ)设直线BC与曲线M的另一交点为D,当点A在以线段CD为直径的圆上时,求直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c为△ABC的三个内角A,B,C的对边,向量 ![]() =(﹣1,
=(﹣1, ![]() ),
), ![]() =(cosA,sinA).若
=(cosA,sinA).若 ![]() ⊥
⊥ ![]() ,且acosB+bcosA=csinC,则角A,B的大小分别为( )
,且acosB+bcosA=csinC,则角A,B的大小分别为( )
A.![]() ,
, ![]()
![]()
B.![]() ,
, ![]()
![]()
C.![]() ,
, ![]()
![]()
D.![]() ,
, ![]()
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的点.
上的点.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中点,且二面角
的中点,且二面角![]() 的余弦值为
的余弦值为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的不等式mx2+2x+6m>0,在下列条件下分别求m的值或取值范围:
(1)不等式的解集为{x|2<x<3};
(2)不等式的解集为R.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com