
分析 (1)由二次函数f(x)=x2+(a-4)x+3-a的对称轴,并结合条件,即可得到对称轴满足的关系式,解之即得实数a的取值范围;
(2)由a的范围即可得到对称轴落在(0,2)内,得到函数在(0,2)上先减后增,分类讨论即可得到函数的最值,依据题意即可求出t的取值范围.
解答 解:函数f(x)=x2+(a-4)x+3-a的对称轴为x=-$\frac{a-4}{2}$,
(1)由于已知f(x)在区间[0,1]上不单调,
则0<-$\frac{a-4}{2}$<1,解得2<a<4,
(2)由于a∈(0,4),则x=-$\frac{a-4}{2}$∈(0,2),
故函数f(x)=x2+(a-4)x+3-a在[0,2]的最小值为$-\frac{(a-2)^{2}}{4}$∈(-1,0),
①当-$\frac{a-4}{2}$∈[1,2),即0<a≤2时,
函数f(x)=x2+(a-4)x+3-a(x∈[0,2])在x=0时取得最大值,
且最大值为3-a,
由于此时0<a≤2,则1≤3-a<3;
②当-$\frac{a-4}{2}$∈(0,1),即2<a<4时,
函数f(x)=x2+(a-4)x+3-a(x∈[0,2])在x=2时取得最大值,
且最大值为22+2(a-4)+3-a=a-1,
由于此时2<a<4,则1<a-1<3;
综上可知,函数f(x)在[0,2]上满足0≤|f(x)|<3,
故若对于任意的a∈(0,4),存在x0∈[0,2],使得|f(x0)|≥t,
则t的取值范围为{t|t≤1}.
点评 本题考查了函数的性质,不等式恒成立问题的转化,属于综合题,有一定的难度.


科目:高中数学 来源: 题型:解答题
 在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ,△ABC的面积为P,正方形面积为Q.求$\frac{P}{Q}$的最小值.
在Rt△ABC内有一内接正方形,它的一条边在斜边BC上,设AB=a,∠ABC=θ,△ABC的面积为P,正方形面积为Q.求$\frac{P}{Q}$的最小值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组名 | 尾号 | 频数 | 频率 |
| 第一组 | 0、1、4 | 200 | 0.2 |
| 第二组 | 3、6 | 250 | 0.25 |
| 第三组 | 2、5、7 | a | b |
| 第四组 | 8、9 | e | 0.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=$\sum_{i=1}^{5}{a}_{i}$,当程序运行一次时:
,其中A的各位数字中,a1=1,且ak(k=2,3,4,5)为0和1的概率分别是$\frac{1}{4}$和$\frac{3}{4}$.记ξ=$\sum_{i=1}^{5}{a}_{i}$,当程序运行一次时:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
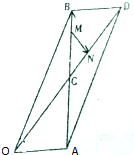 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知正三棱柱ABC-A1B1C1的各棱长均为4,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均为4,E是BC的中点,点F在侧棱CC1上,且CC1=4CF查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\begin{array}{l}{0}\\{0}\end{array})$ | B. | $(\begin{array}{l}{0}\\{1}\end{array})$ | C. | $(\begin{array}{l}{1}\\{0}\end{array})$ | D. | $(\begin{array}{l}{1}\\{1}\end{array})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com