
| A. | 对边相等的四边形一定是平行四边形 | |
| B. | 四边相等的四边形一定是菱形 | |
| C. | 四边相等的四个角也相等的四边形一定是正方形 | |
| D. | 两条对角线互相平分的四边形是平行四边形 |
分析 根据选项中的命题,先判定所表示的四边形是否为平面图形,再判定命题表示的图形是否正确.
解答 解:对于A,对边相等的四边形不一定是平面图形,所以一定是平行四边形,错误;
对于B,四边相等的四边形不一定是平面图形,所以一定是菱形,错误;
对于C,在空间几何中是不成立的.比如你把正四面体去掉任意一对棱后得到的四边形,满足上面的条件,但是不是正方形,
如图所示,AB=BC=CD=DA,∠A=∠ABC=∠C=∠CDA,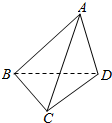
四边相等,四个角也相等,四边形ABCD不是平面图形,所以一定是正方形,错误;
对于D,两条对角线互相平分时,一定相交,所以四边形是平面图形,
对角线互相平分的平面四边形是平行四边形,正确.
故选:D.
点评 本题考查了平面几何中的命题与定理在空间中是否成立的问题,是基础题目.


科目:高中数学 来源: 题型:解答题
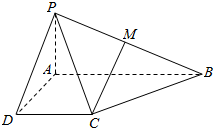 如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.
如图,在四棱锥P-ABCD中,已AB∥CD,AB=2DC,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5 | C. | 9 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 曲线y=f(x)与曲线y=g(x)至多有两个不同的交点 | |
| B. | 曲线y=f(x)与曲线y=g(x)至多有一个交点 | |
| C. | 曲线y=f(x)与曲线y=g(x)恰有两个不同的交点 | |
| D. | 曲线y=f(x)与曲线y=g(x)至少有一个交点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com