
分析 (1)根据相互独立事件概率计算公式列出关于m,n的方程组,能求出结果.
(2)先求出随机变量X的所有可能取值,然后根据独立重复事件的概率计算公式可得到各自的概率,并列出分布列,然后根据数学期望的计算公式能求出结果.
解答 解:由已知得$\left\{\begin{array}{l}{{m}^{2}{n}^{2}=\frac{9}{100}}\\{(1-m)^{2}(1-n)^{2}=\frac{1}{25}}\\{m>n}\end{array}\right.$,
解得m=$\frac{3}{5}$,n=$\frac{1}{2}$.
(2)由题意X的可能取值为0,1,2,3,4,
P(X=0)=$\frac{1}{25}$,
P(X=1)=${C}_{2}^{1}×\frac{3}{5}×(1-\frac{3}{5})×(1-\frac{1}{2})^{2}+(1-\frac{3}{5})^{2}×$${C}_{2}^{1}×\frac{1}{2}×(1-\frac{1}{2})=\frac{1}{5}$,
P(X=2)=${C}_{2}^{1}×\frac{3}{5}×(1-\frac{3}{5})×{C}_{2}^{1}×(1-\frac{1}{2})+(\frac{3}{5})^{2}×$$(1-\frac{1}{2})^{2}+(1-\frac{3}{5})^{2}×(1-\frac{1}{2})^{2}=\frac{37}{100}$,
P(X=3)=${C}_{2}^{1}×\frac{3}{5}×(1-\frac{3}{5})×(\frac{1}{2})^{2}+(\frac{3}{5})^{2}×{C}_{2}^{1}$×$\frac{1}{2}×(1-\frac{1}{2})=\frac{3}{10}$,
P(X=4)=$\frac{9}{100}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{25}$ | $\frac{1}{5}$ | $\frac{37}{100}$ | $\frac{3}{10}$ | $\frac{9}{100}$ |
点评 本题考查相互独立事件的概率、离散型随机变量的分布列和数学期望的求法,考查学生基本的统计知识和综合应用知识的能力,是中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
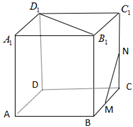 如图,点M,N分别是正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则异面直线B1D1和MN所成的角是( )
如图,点M,N分别是正方体ABCD-A1B1C1D1的棱BC,CC1的中点,则异面直线B1D1和MN所成的角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\sqrt{{x}^{2}}$ | B. | y=$\root{3}{{x}^{3}}$ | C. | y=($\sqrt{x}$)2 | D. | y=$\frac{{x}^{2}}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$)x>($\frac{1}{2}$)y | B. | x-2>y-2 | C. | x${\;}^{\frac{1}{2}}$>y${\;}^{\frac{1}{4}}$ | D. | log0.2x>log0.2y |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| p | q | P∨q | ¬(p∨q) | ¬p | ¬q | (¬p)∧(¬q) |
| 真 | 真 | |||||
| 真 | 假 | |||||
| 假 | 真 | |||||
| 假 | 假 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com