
分析 (1)方法一:(换元法),方法二:(配凑法),
(2)待定系数法.
(3)构造方程组法.
解答 解:(1)方法一:(换元法)设x+1=t,则x=t-1,
∴f(t)=(t-1)2+4(t-1)+1,即f(t)=t2+2t-2.
∴所求函数为f(x)=x2+2x-2.
方法二:(配凑法)f(x+1)=x2+4x+1=(x+1)2+2(x+1)-2
∴所求函数为f(x)=x2+2x-2.
(2)(待定系数法)由题意,设函数为f(x)=ax+b(a≠0)
∵3f(x+1)-f(x)=2x+9,
∴3a(x+1)+3b-ax-b=2x+9,
即2ax+3a+2b=2x+9,
由恒等式性质,得$\left\{\begin{array}{l}{2a=2}\\{3a+2b=9}\end{array}\right.$
∴a=1,b=3.
∴所求函数解析式为f(x)=x+3.
(3)2f(x)+f($\frac{1}{x}$)=3x①
将①中x换成$\frac{1}{x}$,得2f($\frac{1}{x}$)+f(x)=$\frac{3}{x}$②
①×2-②得3f(x)=6x-$\frac{3}{x}$.
∴f(x)=2x-$\frac{1}{x}$.
点评 本题考查的知识点是函数解析式的求解及常用方法,熟练掌握换元法,配凑法,待定系数法,方程组法求解析式的格式和步骤是解答的关键.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {2} | B. | {x|x≤1} | C. | {-$\frac{1}{2}$} | D. | {x|x≤1或x=2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\root{5}{{x}^{5}}$与y=$\sqrt{{x}^{2}}$ | B. | f(x)=x2-2x-1与g(t)=t2-2t-1(t∈z) | ||
| C. | f(x)=$\frac{{x}^{2}-4}{x-2}$与g(x)=x+2 | D. | y=x0与g(x)=$\frac{1}{{x}^{0}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | 9 | C. | -$\frac{1}{9}$ | D. | -9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
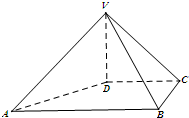 如图,在四棱锥V-ABCD中,VD⊥平面ABCD,VD=DC=BC=2,AB=4,
如图,在四棱锥V-ABCD中,VD⊥平面ABCD,VD=DC=BC=2,AB=4,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com