
【题目】已知{an}是各项均为正数的等比数列,且a1+a2=6,a1a2=a3.
(1)求数列{an}的通项公式;
(2){bn}为各项非零的等差数列,其前n项和为Sn.已知S2n+1=bnbn+1,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】探究与发现:为什么二次函数![]() 的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征
的图象是抛物线?我们知道,平面内与一个定点F和一条定直线l距离相等的点的轨迹是抛物线,这是抛物线的定义,也是其本质特征![]() 因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数
因此,只要说明二次函数的图象符合抛物线的本质特征,就解决了为什么二次函数![]() 的图象是抛物线的问题
的图象是抛物线的问题![]() 进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将
进一步讲,由抛物线与其方程之间的关系可知,如果能用适当的方式将![]() 转化为抛物线标准方程的形式,那么就可以判定二次函数
转化为抛物线标准方程的形式,那么就可以判定二次函数![]() 的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式
的图象是抛物线了.下面我们就按照这个思路来展开.对二次函数式![]() 的右边配方,得
的右边配方,得![]() .由函数图象平移
.由函数图象平移![]() 一般地,设
一般地,设![]() 是坐标平面内的一个图形,将
是坐标平面内的一个图形,将![]() 上所有点按照同一方向,移动同样的长度,得到图形
上所有点按照同一方向,移动同样的长度,得到图形![]() ,这一过程叫作图形的平移
,这一过程叫作图形的平移![]() 的知识可以知道,沿向量
的知识可以知道,沿向量![]() 平移函数
平移函数![]() 的图象
的图象![]() 如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为
如图,函数图象的形状、大小不发生任何变化,平移后图象对应的函数解析式为![]() ,我们把它改写为
,我们把它改写为![]() 的形式
的形式![]() 方程
方程![]() ,这是顶点为坐标原点,焦点为
,这是顶点为坐标原点,焦点为![]() 的抛物线.这样就说明了二次函数
的抛物线.这样就说明了二次函数![]() 的图象是一条抛物线.
的图象是一条抛物线.
请根据以上阅读材料,回答下列问题:
![]() 由函数
由函数![]() 的图象沿向量
的图象沿向量![]() 平移,得到的图象对应的函数解析式为
平移,得到的图象对应的函数解析式为![]() ,求
,求![]() 的坐标;
的坐标;
![]() 过抛物线
过抛物线![]() 的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究
的焦点F的一条直线交抛物线于P、Q两点若线段PF与QF的长分别是p、q,试探究![]() 是否为定值?并说明理由.
是否为定值?并说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
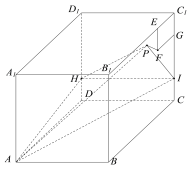
【题目】如图所示,正方体ABCD﹣A1B1C1D1棱长为4,点![]() 在棱
在棱![]() 上,点
上,点![]() 在棱
在棱![]() 上,且
上,且![]() .在侧面
.在侧面![]() 内以
内以![]() 为一个顶点作边长为1的正方形
为一个顶点作边长为1的正方形![]() ,侧面
,侧面![]() 内动点
内动点![]() 满足到平面
满足到平面![]() 距离等于线段
距离等于线段![]() 长的
长的![]() 倍,则当点
倍,则当点![]() 运动时,三棱锥
运动时,三棱锥![]() 的体积的最小值是( )
的体积的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为保障公平性,高考时每个考点都要安装手机屏蔽仪,要求在考点周围1千米处不能收到手机信号,如图,检查员抽查某市一考点![]() ,以考点
,以考点![]() 正西
正西![]() 千米的
千米的![]() 处开始为检查起点,沿着一条北偏东
处开始为检查起点,沿着一条北偏东![]() 方向的公路
方向的公路![]() ,以每小时12千米的速度行驶,并用手机接通电话,问从起点开始计时,最长经过多少分钟检查员开始收不到信号(
,以每小时12千米的速度行驶,并用手机接通电话,问从起点开始计时,最长经过多少分钟检查员开始收不到信号(![]() 点开始),并至少持续多长时间(
点开始),并至少持续多长时间(![]() 之间)该考点才算检查合格?
之间)该考点才算检查合格?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图在直角坐标系中,![]() 的圆心角为
的圆心角为![]() ,
,![]() 所在圆的半径为1,角θ的终边与
所在圆的半径为1,角θ的终边与![]() 交于点C.
交于点C.

(1)当C为![]() 的中点时,D为线段OA上任一点,求
的中点时,D为线段OA上任一点,求![]() 的最小值;
的最小值;
(2)当C在![]() 上运动时,D,E分别为线段OA,OB的中点,求
上运动时,D,E分别为线段OA,OB的中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义在区间![]() 上的两个函数
上的两个函数![]() 和
和![]() ,如果对任意的
,如果对任意的![]() ,均有不等式
,均有不等式![]() 成立,则称函数
成立,则称函数![]() 与
与![]() 在
在![]() 上是“友好”的,否则称为“不友好”的.
上是“友好”的,否则称为“不友好”的.
(1)若![]() ,
,![]() ,则
,则![]() 与
与![]() 在区间
在区间![]() 上是否“友好”;
上是否“友好”;
(2)现在有两个函数![]() 与
与![]() ,给定区间
,给定区间![]() .
.
①若![]() 与
与![]() 在区间
在区间![]() 上都有意义,求
上都有意义,求![]() 的取值范围;
的取值范围;
②讨论函数![]() 与
与![]() 与在区间
与在区间![]() 上是否“友好”.
上是否“友好”.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com