
分析 (I)先利用数量级的定义求出$\overrightarrow{a}•\overrightarrow{b}$,再根据向量数量级的运算性质计算;
(II)求出|2$\overrightarrow{a}$-$\overrightarrow{b}$|2,开方即可.
解答 解:(I)$\overrightarrow{a}•\overrightarrow{b}$=|AB|×|BC|×cos(π-B)=1×2×(-$\frac{1}{2}$)=-1.
${\overrightarrow{a}}^{2}$=|AB|2=1,${\overrightarrow{b}}^{2}$=|BC|2=4,
∴(2$\overrightarrow{a}$-3$\overrightarrow{b}$)•(4$\overrightarrow{a}$+$\overrightarrow{b}$)=8${\overrightarrow{a}}^{2}$-10$\overrightarrow{a}•\overrightarrow{b}$-3${\overrightarrow{b}}^{2}$=6.
(II)∵(2$\overrightarrow{a}-\overrightarrow{b}$)2=4${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=4+4+4=12.
∴|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{12}$=2$\sqrt{3}$.
点评 本题考查了平面向量的数量级运算,属于基础题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 最小值2 | B. | 最大值2 | C. | 最小值1 | D. | 最大值1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a≥3 | B. | a≤3 | C. | a<3 | D. | a>3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
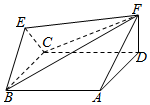 如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.
如图,菱形ABCD与正三角形BCE的边长均为2,它们所在平面互相垂直,FD⊥平面ABCD,且$FD=\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com