
分析 (1)设 f(x)=(x2+x-1)9(2x+1)6 =a0+a1x+a2x2+a3x3+a4x4+…+a24x24,令x=1,可得所有项的系数和.
(2)再令x=-1,可得所有奇次项的系数和减去偶次项的系数和的值,再结合(1)的结果,求得所有偶次项的系数和及所有奇次项的系数和.
解答 解:(1)设 f(x)=(x2+x-1)9(2x+1)6 =a0+a1x+a2x2+a3x3+a4x4+…+a24x24,
令x=1,可得所有项的系数和为 a0+a1+a2 +a3 +a4 +…+a24=36=729 ①,即所有项的系数和为729.
(2)再令x=-1,可得 a0 -a1+a2 -a3 +a4 +…+a22-a23+a24=-1 ②,
由①②求得偶次项的系数和为 a0+a2 +a4 +…+a24=364,所有奇次项的系数和为 a1 +a3 +a5 +…+a23=365.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式的系数和常用的方法是赋值法,属于中档题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
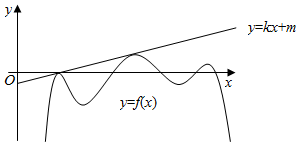
| A. | 2个零点 | B. | 3个极值点 | C. | 2个极大值点 | D. | 3个极大值点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第二、四象限 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 42 | C. | 46 | D. | 56 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{6}+1}{6}$ | B. | $\frac{3-\sqrt{2}}{8}$ | C. | $\frac{3+\sqrt{2}}{8}$ | D. | $\frac{2\sqrt{3}-1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$x2-5y2=1 | B. | 5y2-$\frac{5}{4}$x2=1 | C. | $\frac{5}{4}$y2-5x2=1 | D. | 5x2-$\frac{5}{4}$y2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com