
已知动点P到点F(1,0)的距离比到直线l:x+2=0距离小1.设动点P的轨迹为C,
(Ⅰ)求轨迹C的方程;
(Ⅱ)已知定点M(4,0).斜率为k的直线交轨迹C于A、B两点,使△ABM成为以AB为底边的等腰三角形,
①求斜率k的取值范围;
②求弦长|AB|的最大值.
解:(Ⅰ)设P(x,y),由题意可得,P在直线x+2=0右边,
所以P点到直线x= -1和到F(1,0)距离相等,
所以P点的轨迹是顶点在原点, F为焦点,开口向右的抛物线,
∵F和顶点的距离=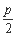 =1,2p=4,所以轨迹C的方程是y²=4x 4分
=1,2p=4,所以轨迹C的方程是y²=4x 4分
(Ⅱ) ①设直线AB的方程为y=kx+b,联立抛物线y2=4x,消元得:k2x2+(2kb-4)x+b2=0,
设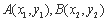 及AB中点为
及AB中点为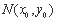 ,
,
则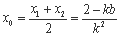 ,y0=kx0+b=
,y0=kx0+b=
∵AM=BM,∴MN⊥AB,∴kMN·kAB= -1,即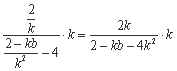 = -1,
= -1,
得2-kb=2k2,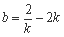 ,
,
由△=-kb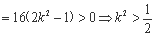 ,
,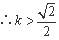 或
或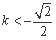 ,
,
②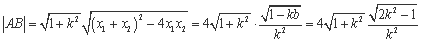
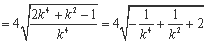
令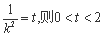 ,
,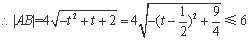
所以弦长的最大值为


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
圆柱的轴截面ABCD是边长为2的正方形,M为正方形ABCD对角线的交点,动点P在圆柱下底面内(包括圆周),若直线AM与直线MP所成角为45°,则点P形成的轨迹为( )
A.椭圆的一部分 B.抛物线的一部分 C.双曲线的一部分 D. 圆的一部分
查看答案和解析>>
科目:高中数学 来源: 题型:
下列命题正确的是( )
A.若x≠kπ,k∈Z,则sin2x+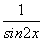 ≥4
≥4
B.若a<0,则a+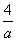 ≥-4
≥-4
C.若a>0,b>0,则lg a+lg b≥2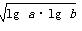
D.若a<0,b<0,则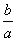 +
+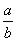 ≥2
≥2
查看答案和解析>>
科目:高中数学 来源: 题型:
从甲、乙等5名志愿者中选出4名,分别从事A,B,C,D四项不同的工作,每人承担一项.若甲、乙二人均不能从事A工作,则不同的工作分配方案共有( )
A.60种 B.72种 C.84种 D.96种
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x)为定义在R上的偶函数,当x≥0时,有f(x+1)=-f(x),且当x∈[0,1)时,f(x)=log2(x+1),给出下列命题:
①f(2 013)+f(-2 014)的值为0;
②函数f(x)在定义域上为周期是2的周期函数;
③直线y=x与函数f(x)的图象有1个交点;
④函数f(x)的值域为(-1,1).
其中正确命题的序号有________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com