
| 价格x | 5 | 5.5 | 6.5 | 7 |
| 销售量y | 12 | 10 | 6 | 4 |
分析 (1)根据回归系数公式计算回归系数;
(2)把y=13代入回归方程计算x.
解答 解:(Ⅰ)$\overline{x}$=$\frac{5+5.5+6.5+7}{4}$=6,$\overline{y}$=$\frac{12+10+6+4}{4}$=8.
$\sum_{i=1}^{4}{x}_{i}{y}_{i}$=5×12+5.5×10+6.5×6+7×4=182,
$\sum_{i=1}^{4}{{x}_{i}}^{2}$=52+5.52+6.52+72=146.5,
$\stackrel{∧}{b}$=$\frac{182-4×6×8}{146.5-4×{6}^{2}}$=-4,$\stackrel{∧}{a}$=8+4×6=32.
∴销售量y对奶茶的价格x的回归直线方程为$\stackrel{∧}{y}$=-4x+32.
(Ⅱ)令-4x+32=13,解得x=4.75.
答:商品的价格定为4.75元.
点评 本题考查了线性回归方程的解法和数值估计,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
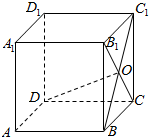 如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.
如图,在正方体ABCD-A1B1C1D1中,B1C和BC1相交于点O,若$\overrightarrow{DO}=x\overrightarrow{DA}+y\overrightarrow{DC}+z\overrightarrow{D{D_1}}$,则$\frac{x}{y}$=$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $2\sqrt{5}-1$ | C. | $2\sqrt{5}+1$ | D. | $2\sqrt{5}-2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com