Question

5．已知P为抛物线y²=4x上的任意一点，记点P到y轴的距离为d，对给定点A（3，4），则|PA|+d的最小值为（　　）

• A． $2\sqrt{5}$
• B． $2\sqrt{5}-1$
• C． $2\sqrt{5}+1$
• D． $2\sqrt{5}-2$

Answer 1

分析 可设抛物线的焦点为F（1，0），根据抛物线的定义，当|PA|+d最小时，|PA|+|PF|最小，从而问题转化为求|PA|+|PF|的最小值，而由图形便可看出|PA|+|PF|的最小值为|AF|，而|AF|=$2\sqrt{5}$，这样便可得出|PA|+d的最小值．

解答 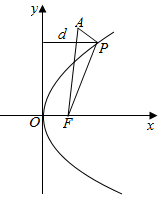解：如图，设抛物线焦点F（1，0）；
|PA|+d最小时，|PA|+d+1最小；
根据抛物线的定义，d+1=|PF|；
∴只要求|PA|+|PF|的最小值即可；
由图看出，连接AF，当P点为AF和抛物线交点时，|PA|+|PF|最小；
且最小值为|AF|=$\sqrt{4+16}=2\sqrt{5}$；
∴|PA|+d+1的最小值为$2\sqrt{5}$；
∴|PA|+d的最小值为$2\sqrt{5}-1$．
故选：B．

点评 考查数形结合解题的方法，抛物线的标准方程，根据抛物线的标准方程能求出抛物线的焦点坐标，以及抛物线的定义，两点间的距离公式．