已知函数f(x)=a(x2+1)+lnx.
(Ⅰ)讨论函数f′(x)>0的单调性;
(Ⅱ)若对任意a∈(-4,-2)及x∈[1,3]时,恒有ma-f(x)>a2成立,求实数m的取值范围.
解:(Ⅰ)f′(x)=2ax+

=
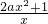
(x>0),
①当a≥0时,恒有f'(x)>0,则f′(x)>0在(0,+∞)上是增函数;
②当a<0时,当
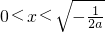
时,f'(x)>0,则f(x)在
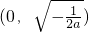
上是增函数;
当
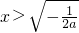
时,f'(x)<0,则f(x)在
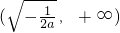
上是减函数;
综上,当a≥0时,f(x)在(0,+∞)上是增函数;当a<0时,f(x)在
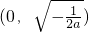
上是增函数,在
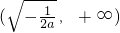
上是减函数.
(Ⅱ)由题意知对任意a∈(-4,-2)及x∈[1,3]时,恒有ma-f(x)>a
2成立,
等价于ma-a
2>f(x)
max,
因为a∈(-4,-2),所以
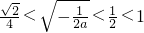
由(Ⅰ)知:当a∈(-4,-2)时,f(x)在[1,3]上是减函数,
所以f(x)
max=f(1)=2a,
所以ma-a
2>2a,即m<a+2,
因为a∈(-4,-2),所以-2<a+2<0,
所以实数m的取值范围为m≤-2.
分析:(Ⅰ)先求出f′(x),分a≥0、a<0两种情况讨论解不等式f'(x)>0,f'(x)<0可求得单调区间;
(Ⅱ)对任意x∈[1,3]时,恒有ma-f(x)>a
2成立,等价于ma-a
2>f(x)
max,由(Ⅰ)知f(x)的单调性,根据单调性易求f(x)
max,转化为关于a的不等式,分离出参数m后,再求关于a的函数的最值即可;
点评:本题考查利用导数研究函数的单调性、最值,考查恒成立问题,考查转化思想,转化为函数最值是解决恒成立问题的常用方法.

 =
=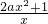 (x>0),
(x>0),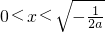 时,f'(x)>0,则f(x)在
时,f'(x)>0,则f(x)在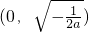 上是增函数;
上是增函数;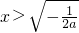 时,f'(x)<0,则f(x)在
时,f'(x)<0,则f(x)在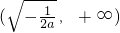 上是减函数;
上是减函数;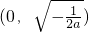 上是增函数,在
上是增函数,在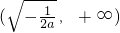 上是减函数.
上是减函数.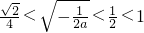


 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案