
���� ��1������֪��${F}_{1}��-\sqrt{3}��0��$��H��-$\frac{8\sqrt{3}}{7}$��-$\frac{b}{7}$�����ɴ��������ԲC�ķ��̣�
��2����������ֱ��l�ķ���Ϊy=k��x-1������$\left\{\begin{array}{l}{y=k��x-1��}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$���ã�4k2+1��x2-8k2x+4k2-4=0���ɴ�����Τ�ﶨ����ֱ�߷��̡���Բ���ʣ������֪������֤��k•k��Ϊ��ֵ��
��� �⣺��1������ԲC�Ľ���Ϊ2$\sqrt{3}$����${F}_{1}��-\sqrt{3}��0��$��
��D��0��b����ֱ��DF1����ԲC����һ����ΪH����|DF1|=7|F1H|��
���H��-$\frac{8\sqrt{3}}{7}$��-$\frac{b}{7}$����
��$\frac{64��3}{49{a}^{2}}$+$\frac{1}{49}=1$�����a2=4����b2=a2-3=1��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}+{y}^{2}=1$��
֤������2����������ֱ��l�ķ���Ϊy=k��x-1����
��$\left\{\begin{array}{l}{y=k��x-1��}\\{{x}^{2}+4{y}^{2}-4=0}\end{array}\right.$���ã�4k2+1��x2-8k2x+4k2-4=0��
��E��x1��y1����F��x2��y2������${x}_{1}+{x}_{2}=\frac{8{k}^{2}}{4{k}^{2}+1}$��${x}_{1}{x}_{2}=\frac{4{k}^{2}-4}{4{k}^{2}+1}$��
ֱ��AE��AF�ķ��̷ֱ�Ϊy=$\frac{{y}_{1}}{{x}_{1}-2}��x-2��$��$y=\frac{{y}_{2}}{{x}_{2}-2}$��x-2����
��x=3����M��3��$\frac{{y}_{1}}{{x}_{1}-2}$����N��3��$\frac{{y}_{2}}{{x}_{2}-2}$����
��P��3��$\frac{1}{2}��\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2}��$����
��k•k��=$\frac{k}{4}��$$\frac{k��{x}_{1}-1����{x}_{2}-2��+k��{x}_{2}-1����{x}_{1}-2��}{��{x}_{1}-2����{x}_{2}-2��}$
=$\frac{{k}^{2}}{4}$��$\frac{2{x}_{1}{x}_{2}-3��{x}_{1}+{x}_{2}��+4}{{x}_{1}{x}_{2}-2��{x}_{1}+{x}_{2}��+4}$
=$\frac{{k}^{2}}{4}$��$\frac{\frac{8{k}^{2}-8-24{k}^{2}+16{k}^{2}+4}{4{k}^{2}+1}}{\frac{4{k}^{2}-4-16{k}^{2}+16{k}^{2}+4}{4{k}^{2}+1}}$
=$\frac{{k}^{2}}{4}��\frac{��-4��}{4{k}^{2}}$
=-$\frac{1}{4}$��
��k•k��Ϊ��ֵ-$\frac{1}{4}$��
���� ���⿼����Բ���̵���������ֱ�ߵ�б�ʵij˻�Ϊ��ֵ��֤�������е��⣬����ʱҪ�������⣬ע��ֱ�߷��̡���Բ���ʵĺ������ã�


 ��������ϵ�д�
��������ϵ�д� ����˼ά����ѵ����ʱ��ѧ��ϵ�д�
����˼ά����ѵ����ʱ��ѧ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{3\sqrt{2}}}{8}$ | B�� | $\frac{{5\sqrt{2}}}{8}$ | C�� | $\frac{{7\sqrt{2}}}{8}$ | D�� | $\frac{{\sqrt{2}}}{8}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
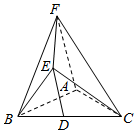 ����ͼ��ʾ�ļ�����EFABC�У���֪��ABC�ǵ��������Σ�AB=AC��AF��ƽ��ABC��DΪBC���е㣬DE��AF��BC=AF=2DE=2��
����ͼ��ʾ�ļ�����EFABC�У���֪��ABC�ǵ��������Σ�AB=AC��AF��ƽ��ABC��DΪBC���е㣬DE��AF��BC=AF=2DE=2���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com