Question

10．正面体ABCD的体积为V，P是正四面体ABCD的内部的点．
①设“V_P-ABC≥$\frac{1}{4}$V”的事件为X，则概率P（X）=$\frac{27}{64}$；
②设“V_P-ABC≥$\frac{1}{4}$V且V_P-BCD≥$\frac{1}{4}$V”的事件为Y，则概率P（Y）=$\frac{1}{8}$．

Answer 1

分析 首先确定点P的区域，即区域D；然后确定所求的事件中的点所在区域d；分别计算区域D和d的体积；最后计算所求概率为$\frac{d的测度}{D的测度}$．

解答 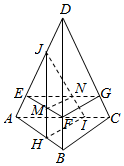解：（1）如图所示，
分别取DA、DB、DC上的点E、F、G，
并使DE=3EA，DF=3FB，DG=3GC，并连结EF、FG、GE，
则平面EFG∥平面ABC；
当P在正四面体DEFG内部运动时，
满足V_PABC≥$\frac{1}{4}$V，故P（X）=$\frac{{V}_{DEFG}}{{V}_{DABC}}$=${（\frac{DE}{DA}）}^{3}$=${（\frac{3}{4}）}^{3}$=$\frac{27}{64}$；
（2）在AB上取点H，使AH=3HB，在AC上取点I，
使AI=3IC，在AD上取点J，使AJ=3JD，
则P在正四面体AHIJ内部运动时，满足V_PBCD≥$\frac{1}{4}$V；
设JH交EF于M，JI交EG于N，则面MIN∥面BCD．
结合（1），当P在正四面体DFEG的内部及正四面体AHIJ的内部运动，
也即P在正四面体EMNJ内部运动时，同时满足V_PABC≥$\frac{1}{4}$V且V_PBCD≥$\frac{1}{4}$V，
于是P（Y）=$\frac{{V}_{JEMN}}{{V}_{DABC}}$=${（\frac{JE}{DA}）}^{3}$=${（\frac{1}{2}）}^{3}$=$\frac{1}{8}$．

点评 本题考查了几何概型的应用问题，也考查了数形结合的应用问题，解题的关键是确定点P所表示的区域，是综合性题目．