
| A. | (-1,$\frac{1}{3}$) | B. | (-∞,-1)∪($\frac{1}{3}$,+∞) | C. | [1-$\frac{π}{2}$,$\frac{1}{3}$) | D. | (-1,$\frac{π}{4}$) |
分析 求出函数的导数,得到函数的单调性,结合函数的奇偶性得到关于x的不等式,解出即可.
解答 解:f′(x)=sinx+xcosx-sinx=xcosx,
x∈[-$\frac{π}{2}$,0)时,cosx>0,f′(x)<0,
x∈(0,$\frac{π}{2}$]时,cosx≥0,f′(x)≥0,
故f(x)在[-$\frac{π}{2}$,0)递减,在(0,$\frac{π}{2}$]递增,
而f(-x)=xsinx+cosx=f(x),f(x)是偶函数,
不等式f(2x)<f(x-1),
即|2x|<|x-1|,解得:-1<x<$\frac{1}{3}$,
而$\left\{\begin{array}{l}{-\frac{π}{2}≤2x≤\frac{π}{2}}\\{-\frac{π}{2}≤x-1≤\frac{π}{2}}\end{array}\right.$,解得:1-$\frac{π}{2}$≤x≤$\frac{π}{4}$,
综上,1-$\frac{π}{2}$≤x<$\frac{1}{3}$,
故选:C.
点评 本题考查了函数的单调性、奇偶性问题,考查导数的应用,是一道中档题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源:2017届重庆市高三10月月考数学(文)试卷(解析版) 题型:选择题
已知抛物线 的焦点到双曲线
的焦点到双曲线 的渐近线的距离不大于
的渐近线的距离不大于 ,则双曲线
,则双曲线 的离心率的取值范围是( )
的离心率的取值范围是( )
A. B.
B.
C.  D.
D.
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{14}$ | B. | 5 | C. | $\sqrt{31}$ | D. | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {-3,-1,0} | C. | {-1,0,2} | D. | {-3,0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
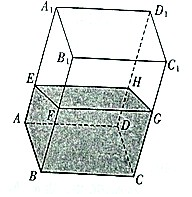 如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:
如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌满一些水(未满),现将容器底面一边BC固定在地面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:| A. | 1个 | B. | 2个 | C. | 3 个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com