
| A. | $(0,\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(\frac{{\sqrt{2}}}{2},1)$ | D. | $(\sqrt{2},+∞)$ |
分析 求出渐近线方程及准线方程;求得它们的交点A,B的坐标;利用圆内的点到圆心距离小于半径,列出参数a,b,c满足的不等式,求出离心率的范围.
解答 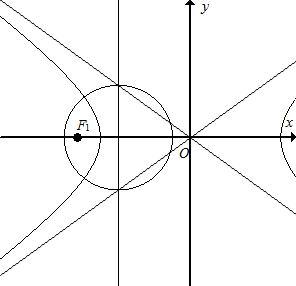 解:双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的渐近线y=±$\frac{b}{a}$x,准线x=±$\frac{{a}^{2}}{c}$,
解:双曲线$E:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1\;(a>0,b>0)$的渐近线y=±$\frac{b}{a}$x,准线x=±$\frac{{a}^{2}}{c}$,
求得A(-$\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),B(-$\frac{{a}^{2}}{c}$,-$\frac{ab}{c}$),
左焦点在以AB为直径的圆内,
得出-$\frac{{a}^{2}}{c}$+c<$\frac{ab}{c}$,
∴b<a,
∴c2<2a2
∴1<e<$\sqrt{2}$,
故选:B.
点评 本题考查双曲线的准线、渐近线方程形式、考查圆内的点满足的不等条件、注意双曲线离心率本身要大于1.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9×10 n-1个 | B. | 9×10 n个 | C. | 9×10 n+1个 | D. | 9×10 n+2个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(\frac{1}{2},\frac{{\sqrt{3}}}{2})$ | B. | $(-\frac{{\sqrt{3}}}{2},-\frac{1}{2})$ | C. | $(-\frac{1}{2},-\frac{{\sqrt{3}}}{2})$ | D. | $(-\frac{{\sqrt{3}}}{2},\frac{1}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 30° | C. | 135° | D. | 45° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com