
分析 (1)设x2=t,根据函数f(t)的定义域为得出t的取值范围,再求出x的取值范围即可;
(2)设2x+1=t,根据函数f(2x+1)的定义域求出t的取值范围即可.
解答 解:(1)设x2=t,
由题意,函数f(t)的定义域为(0,1),
即0<t<1,∴0<x2<1,
解得-1<x<0或0<x<1;
∴f(x2)的定义域为(-1,0)∪(0,1);
(2)设2x+1=t,则x=$\frac{t-1}{2}$,
∵函数f(2x+1)的定义域为(0,1),
∴0<$\frac{t-1}{2}$<1,
解得1<t<3,
∴f(t)的定义域是(1,3),
即f(x)的定义域是(1,3).
点评 本题考查了函数的定义域和应用问题,是基础题目.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
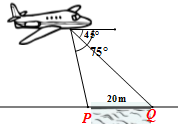 如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.
如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(\frac{{\sqrt{2}}}{2},1)$ | D. | $(\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,1] | B. | [-1,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$] | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com