
分析 (1)求导数,利用f(x)在( 0,2 )上无极值,得到m-1=1,即可求实数m的值;
(2)令f′(m)=0得 x=1,或 x=m-1,分类讨论,确定函数的单调性,利用f(x0)是f(x)在[0,2]上的最大值,求实数m的取值范围;
(3)若不等式$\frac{f(x)}{e^x}≥2lnx-\frac{1}{x^2}+2m+1$对于任意0<x≤1恒成立,即是$m≤x+\frac{1}{x^3}-\frac{2lnx}{x}-2$对于任意0<x≤1恒成立,构造函数求最值,即可求实数m的取值范围.
解答 解:(1)∵f(x)=ex[x2-(m+2)x+2m+1]
∴f′(x)=ex•[x2-mx+(m-1)]=(x-1)[x-(m-1)]•ex,
∵f(x)在( 0,2 )上无极值
∴m-1=1得m=2…(3分)
(2)∵存在实数x0∈(0,2),使得f(x0)是f ( x )在[0,2]上的最大值
∴x∈[0,2]时,f(x)在x=x0处取得最大值
由(1)得f′(x)=(x-1)[x-(m-1)]•ex
令f′(m)=0得 x=1,或 x=m-1
①当1<m<2时,0<m-1<1,
则f(x)在(0,m-1)上单调递增,在(m-1,1)上单调递减,在(1,2)上单调递增,
∴$\left\{{\begin{array}{l}{f(m-1)≥f(2)}\\{1<m<2}\end{array}}\right.$得 (4-m)em-1≥e2即 (4-m)em≥e3,
令g(m)=(4-m)em则 g′(m)=(3-m)em,
由1<m<2得g′(m)>0,∴g(m)在(1,2)上单调递增,∴g(m)<g(2)<g(3)=e3,
∴g(m)在1<m<2时无解,故舍去;
②当m=2时,m-1=1f(x)在(0,2)上单调递增,${f_{max}}(x)=f(2)={e^2}$,不合题意,舍去;
③当2<m<3时,1<m-1<2f(x)在(0,1)上单调递增,在(1,m-1)上单调递减,在(m-1,2)上单调递增,
∴$\left\{{\begin{array}{l}{f(1)≥f(2)}\\{2<m<3}\end{array}}\right.$即$\left\{{\begin{array}{l}{me≥{e^2}}\\{2<m<3}\end{array}}\right.$,∴e≤m<3.
④当m≥3时,m-1≥2f(x)在(0,1)上单调递增,在(1,2)上单调递减,符合题意;
综上所述:m≥e.…(8分)
(3)由不等式$\frac{f(x)}{e^x}≥2lnx-\frac{1}{x^2}+2m+1$,
即是$m≤x+\frac{1}{x^3}-\frac{2lnx}{x}-2$对于任意0<x≤1恒成立
令$h(x)≤x+\frac{1}{x^3}-\frac{2lnx}{x}-2$(0<x≤1)
则${h^'}(x)=1-\frac{3}{x^4}-\frac{2(1-lnx)}{x^2}=\frac{{{x^4}-3-2{x^2}(1-lnx)}}{x^4}$
∵0<x≤1,
∴x4-3<0,-2x2(1-lnx)<0∴h′(x)<0,
∴h(x)在(0,1]上单调递减,∴hmin(x)=h(1)=0
∴m的取值范围是m≤0.…(12分)
点评 本题考查导数知识的综合运用,考查函数的极值、单调性,考查恒成立问题,考查学生分析解决问题的能力,难度大.


科目:高中数学 来源: 题型:解答题
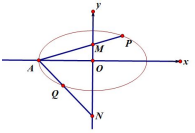 在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.
在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)的图象过点(0,$\frac{1}{2}$) | B. | f(x)在$[{\frac{π}{6},\frac{2π}{3}}]$上是减函数 | ||
| C. | f(x)的一个对称中心是$({\frac{5π}{12},0})$ | D. | f(x)的图象的一条对称轴是x=$\frac{5π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com