
分析 (1)根据题意可写出下调电价后新增的用电量,从而可得电力部门收益y与实际电价x间的函数关系式;
(2)根据(1)中建立的函数,求导,令导数等于0,分析单调性即可得解.
(3)求出x=0.64时的函数值,进行比较,最大的就是最大值.
解答 解:(1)设下调后的电价为x元/(kW•h),
依题意知用电量增至1+50(x-0.8)2,
电力部门的收益为:y=[1+50(x-0.8)2](x-0.5),0.5<x<0.8.
(2)由(1)知:y=[1+50(x-0.8)2](x-0.5)=50x3-105x2+73x-16.5,0.5<x<0.8,
∴y′=150x2-210x+73.
令y′=0,解得x=0.76,或x=0.64.
可得:当0.5<x<0.64时函数递增;
当0.64<x<0.76时函数递减;
当0.76<x<0.8时函数递增;
x=0.64,x=0.76为函数的极值点;
(3)由(2)知电力部门将电价定位0.64元/(kW.h)时,
可以获得最大受益,最大受益为0.3192亿元.
点评 本题主要考查实际问题中的数据提取和分析能力,考查导数再求函数最大值中的应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在${x_0}∈R,x_0^2+2{x_0}+2<0$ | B. | 存在${x_0}∉R,x_0^2+2{x_0}+2<0$ | ||
| C. | 任意x∈R,x2+2x+2<0 | D. | 任意x∉R,x2+2x+2<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
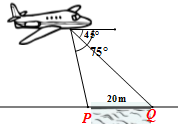 如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.
如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(\frac{{\sqrt{2}}}{2},1)$ | D. | $(\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com