
分析 由复合函数求导法则及导数的运算,求得f′(x),将x=$\frac{3}{2}$,代入f′(x),即可求得f′($\frac{3}{2}$).
解答 解:f(x)=$\frac{ln(2x-1)}{x}$,f′(x)=$\frac{\frac{2x}{2x-1}-ln(2x-1)}{{x}^{2}}$=$\frac{2x-(2x-1)ln(2x-1)}{(2x-1){x}^{2}}$,
f′($\frac{3}{2}$)=$\frac{2×\frac{3}{2}-(2×\frac{3}{2}-1)ln(2×\frac{3}{2}-1)}{(2×\frac{3}{2}-1)×\frac{9}{4}}$=$\frac{6-4ln2}{9}$,
故答案为:$\frac{6-4ln2}{9}$.
点评 本题考查复合函数求导法则及导数运算法则,考查计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -$\frac{1}{2}$或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 存在${x_0}∈R,x_0^2+2{x_0}+2<0$ | B. | 存在${x_0}∉R,x_0^2+2{x_0}+2<0$ | ||
| C. | 任意x∈R,x2+2x+2<0 | D. | 任意x∉R,x2+2x+2<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
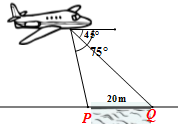 如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.
如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com