
分析 (I)利用导数的几何意义求出切线的斜率,代入点斜式方程即可;
(II)令g(x)=f(x)-x-1,求出gmax(x),令gmax(x)<0解出a的范围;
(III)判断f(x)的单调性,得出f(x1),f(x2),f(x1+x2)的大小关系,根据导数的运算性质和不等式的性质得出结论.
解答 解:(Ⅰ)当a=e2时,f(x)=x(2-lnx),f'(x)=2-lnx-1,
切线l的斜率k=f'(1)=2-ln1-1=1,又f(1)=2-ln1=2,
所以切线l的方程为y=x+1.
(Ⅱ)由题知f(x)-x-1<0对于x>0恒成立,即x(lna-lnx)<0对于x>0恒成立,
令g(x)=x(lna-lnx)-x-1,则g'(x)=lna-lnx-2,由g'(x)=0得x=$\frac{a}{{e}^{2}}$,
| x | (0,$\frac{a}{{e}^{2}}$) | $\frac{a}{{e}^{2}}$ | ($\frac{a}{{e}^{2}}$,+∞) |
| g'(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |
点评 本题考查了导数的几何意义,导数与函数单调性的关系,函数最值的计算,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
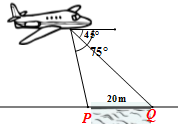 如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.
如图,从一架飞机上观察前下方河流两岸P、Q两点的俯角分别为75°、45°,已知河的宽度|PQ|=20m,则此时飞机的飞行高度为$10(\sqrt{3}+1)$m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,\sqrt{2})$ | B. | $(1,\sqrt{2})$ | C. | $(\frac{{\sqrt{2}}}{2},1)$ | D. | $(\sqrt{2},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,1] | B. | [-1,$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,$\frac{1}{2}$] | D. | ($\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com