
| A. | 18 | B. | 20 | C. | 21 | D. | 22 |
分析 解:根据题意,分2种情况讨论:①、若A与C之间为B,即B在A、C中间且三人相邻,②、若A与C之间不是B,分别求出每种情况的排法数目,由分类计数原理计算可得答案.
解答 解:根据题意,分2种情况讨论:
①、若A与C之间为B,即B在A、C中间且三人相邻,
考虑A、C的顺序,有A22种情况,将三人看成一个整体,
与D、E2人全排列,有A33=6种情况,
则此时有2×6=12种排法;
②、若A与C之间不是B,
先D、E中选取1人,安排A、C之间,有C21=2种选法,
此时B在A的另一侧,将4人看成一共整体,考虑之间的顺序,有A22=2种情况,
将这个整体与剩余的1人全排列,有A22=2种情况,
则此时有2×2×2=8种排法;
则一共有12+8=20种符合题意的排法;
故选:B.
点评 本题考查排列、组合的综合应用,涉及分类计数原理的应用,注意“A与B相邻且A与C之间恰好有一名同学”这一条件.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
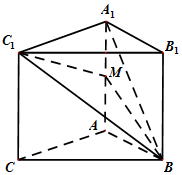 如图,在直三棱柱ABC-A1B1C1中,若四边形AA1C1C是边长为4的正方形,且AB=3,BC=5,M是AA1的中点,则三棱锥A1-MBC1的体积为4.
如图,在直三棱柱ABC-A1B1C1中,若四边形AA1C1C是边长为4的正方形,且AB=3,BC=5,M是AA1的中点,则三棱锥A1-MBC1的体积为4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com