
【题目】已知数列{![]() }的前n项和为Sn,
}的前n项和为Sn,![]() ,且对任意的n∈N*,n≥2都有
,且对任意的n∈N*,n≥2都有![]() 。
。
(1)若![]() 0,
0,![]() ,求r的值;
,求r的值;
(2)数列{![]() }能否是等比数列?说明理由;
}能否是等比数列?说明理由;
(3)当r=1时,求证:数列{![]() }是等差数列。
}是等差数列。
【答案】(1)1;(2)不可能是等比数列;(3)详见解析.
【解析】
(1)令![]() ,得到
,得到![]() ,再将和用项来表示,再结合条件,求得结果;
,再将和用项来表示,再结合条件,求得结果;
(2)假设其为等比数列,利用![]() ,结合
,结合![]() ,得到关于
,得到关于![]() 的方程,求解得出
的方程,求解得出![]() 或
或![]() ,将其回代检验得出答案;
,将其回代检验得出答案;
(3)将r=1代入上式,类比着写出![]() ,两式相减得到
,两式相减得到![]() ,进一步凑成
,进一步凑成![]() ,结合
,结合![]() ,从而证得数列
,从而证得数列![]() 是以
是以![]() 为首项,2
为首项,2![]() 为公差的等差数列.
为公差的等差数列.
(1)令n=2,得:![]() ,
,
即:![]() ,
,
化简,得:![]() ,因为,
,因为,![]() ,
,![]() ,
,
所以,![]() ,解得:r=1.
,解得:r=1.
(2)假设![]() 是等比数列,公比为
是等比数列,公比为![]() ,则
,则![]() ,且
,且![]() ,
,
解得![]() 或
或![]() ,
,
由![]() ,
,
可得![]() ,
,
所以![]() ,
,
两式相减,整理得![]() ,
,
两边同除以![]() ,可得
,可得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以上式不可能对任意![]() 恒成立,故
恒成立,故![]() 不可能是等比数列.
不可能是等比数列.
(3)![]() 时,令
时,令![]() ,整理得
,整理得![]() ,
,
又由![]() 可知
可知![]() ,
,
令![]() ,可得
,可得![]() ,解得
,解得![]() ,
,
由(2)可知![]() ,
,
所以![]() ,
,
两式相减,整理得![]() ,
,
所以![]() ,
,
两式相减,可得![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,又因为
,又因为![]() ,
,
所以数列![]() 是以
是以![]() 为首项,2
为首项,2![]() 为公差的等差数列.
为公差的等差数列.


科目:高中数学 来源: 题型:
【题目】圆O:x2+y2=8内有一点P(﹣1,2),AB为过点P且倾斜角为α的弦,
(1)当α=135°时,求AB的长;
(2)当弦AB被点P平分时,写出直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据被墨迹污损不清(如图1),但甲得分的折线图完好(如图2),则下列结论错误的是( )
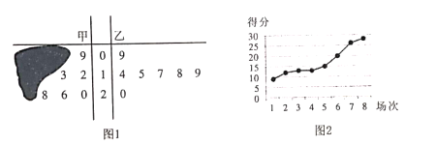
A.乙运动员得分的中位数是17,甲运动员得分的极差是19
B.甲运动员发挥的稳定性比乙运动员发挥的稳定性差
C.甲运动员得分有![]() 的叶集中在茎1上
的叶集中在茎1上
D.甲运动员得分的平均值一定比乙运动员得分的平均值低
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设关于某设备的使用年限x(年)和所支出的维修费用y万元有如下的统计资料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)画出散点图并判断是否线性相关;
(2)如果线性相关,求线性回归方程;
(3)估计使用年限为10年时,维修费用是多少?
附注:①参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,
,![]() 为抛物线
为抛物线![]() 上异于原点的任意一点,过点
上异于原点的任意一点,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴的正半轴于点
轴的正半轴于点![]() ,且有
,且有![]() .当点
.当点![]() 的横坐标为3时,
的横坐标为3时,![]()
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)若直线![]() ,且
,且![]() 和抛物线
和抛物线![]() 有且只有一个公共点
有且只有一个公共点![]() ,试问直线
,试问直线![]() (
(![]() 为抛物线
为抛物线![]() 上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
上异于原点的任意一点)是否过定点,若过定点,求出定点坐标;若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() ,
,![]() .
.
(1)若集合![]() 含有三个元素,且
含有三个元素,且![]() ,这样的集合
,这样的集合![]() 有多少个?所有集合
有多少个?所有集合![]() 中个元素之和是多少?
中个元素之和是多少?
(2)若集合![]() 各含有三个元素,且
各含有三个元素,且![]() ,
,![]() ,
,![]() ,这样的集合
,这样的集合![]() 有多少种配对方式?
有多少种配对方式?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P在抛物线x2=2y上,过点P作x轴的垂线,垂足为H,动点Q满足![]() .
.
(1)求动点O的轨迹E的方程;
(2)点M(-4,4),过点N(4,5)且斜率为k的直线交轨迹E于A,B两点,设直线MA,MB的斜率分别为k1,k2,求k1k2的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com