Question

在△ABC中，D为BC边上的中点，P_o是边AB上的一个定点，P_oB=

1

4

AB，且对于AB上任一点P，恒有

PB

•

PC

≥

PoB

•

PoC

，则下列结论正确的是

 

（填上所有正确命题的序号）．
①当P与A，B不重合时，

PB

+

PC

与

PD

共线；
②

PB

•

PC

=

PD2

-

DB2

；
③存在点P，使|

PD

|＜|

PoD

|；
④

PoC

•

AB

=0；
⑤AC=AB．

Answer 1

考点：平面向量数量积的运算

专题：计算题,平面向量及应用

分析：以AB所在的直线为x轴，以AB的中垂线为y轴建立直角坐标系，设AB=4，C（a，b），P（x，0），A（-2，0），B（2，0），P₀（1，0），D（

2+a

2

，

b

2

），然后由题意可写出结合向量的数量积的坐标表示可得关于x的二次不等式，结合二次不等式的知识可求a=0，进而可判断⑤；由向量的中点表示，即可判断①；
运用数列的坐标表示，求出

PB

•

PC

，向量的模的公式，求得

PD2

-

DB2

即可判断②；
求出|

PD

|，|

PoD

|，即可判断③；运用向量的数量积的坐标公式，求出

PoC

•

AB

，即可判断④．

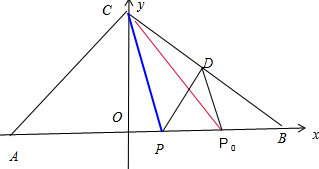
解答： 解：以AB所在的直线为x轴，以AB的中垂线为y轴建立直角坐标系
设AB=4，C（a，b），P（x，0）（-2＜x＜2），
则BP₀=1，A（-2，0），B（2，0），P₀（1，0），D（

2+a

2

，

b

2

），
∴

P0B

=（1，0），

PB

=（2-x，0），

PC

=（a-x，b），

P0C

=（a-1，b）
∵恒有

PB

•

PC

≥

PoB

•

PoC

，∴（2-x）（a-x）≥a-1恒成立，
整理可得x²-（a+2）x+a+1≥0恒成立，
令f（x）=x²-（a+2）x+a+1，
当

a+2

2

＜-2，必有f（-2）≥0，无解；
当

a+2

2

＞2，必有f（2）≥0，无解；
当-2≤

a+2

2

≤2，必有△=（a+2）²-4（a+1）≤0
即△=a²≤0，∴a=0，即C在AB的垂直平分线上，
∴AC=BC，故△ABC为等腰三角形．
故⑤错误；
对于①，当P与A，B不重合时，

PB

+

PC

=（2+a-2x，b），

PD

=（

2+a-2x

2

，

b

2

），即有

PD

=

1

2

（

PB

+

PC

），则有

PB

+

PC

与

PD

共线，故①正确；
对于②，

PB

•

PC

=（2-x）（a-x）=x²-2x，

PD2

-

DB2

=（

2+a-2x

2

）²-（

a-2

2

）²-（

b

2

）²
=（1-x）²-1-

b2

4

＜x²-2x，故②错误；
对于③，|

PD

|=

(1-x)2+ b2 4

＞|

PoD

|=

b2 4

，则不存在点P，使|

PD

|＜|

PoD

|，故③错误；
对于④，

PoC

•

AB

=（-1，b）•（4，0）=-4+0=-4，故④错误．
故答案为：①．

点评：本题主要考查了平面向量的运算，向量的模及向量的数量积的概念，向量运算的几何意义的应用，还考查了利用向量解决简单的几何问题的能力．